题目内容
已知,抛物线y=ax2+x+c的顶点为M(-1,-2),它与x轴交于点B,C(点B在点C左侧).

(1)求点B、点C的坐标;
(2)将这个抛物线的图象沿x轴翻折,得到一个新抛物线,这个新抛物线与直线l:y=-4x+6交于点N.
①求证:点N是这个新抛物线与直线l的唯一交点;
②将新抛物线位于x轴上方的部分记为G,将图象G以每秒1个单位的速度向右平移,同时也将直线l以每秒1个单位的速度向上平移,记运动时间为t,请直接写出图象G与直线l有公共点时运动时间t的范围.

(1)求点B、点C的坐标;
(2)将这个抛物线的图象沿x轴翻折,得到一个新抛物线,这个新抛物线与直线l:y=-4x+6交于点N.
①求证:点N是这个新抛物线与直线l的唯一交点;
②将新抛物线位于x轴上方的部分记为G,将图象G以每秒1个单位的速度向右平移,同时也将直线l以每秒1个单位的速度向上平移,记运动时间为t,请直接写出图象G与直线l有公共点时运动时间t的范围.
考点:二次函数综合题
专题:
分析:(1)根据题意可以设抛物线的顶点式方程为y=a(x+1)2-2,然后根据顶点坐标公式来求a的值即可;
(2)①根据翻折变换的性质求得点新抛物线的顶点坐标M′(-1,2).则根据顶点式方程和点C的坐标可以求得新抛物线的解析式为y=-
x2-x+
.然后求新抛物线与直线l的交点即可;
②当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点.
(2)①根据翻折变换的性质求得点新抛物线的顶点坐标M′(-1,2).则根据顶点式方程和点C的坐标可以求得新抛物线的解析式为y=-
| 1 |
| 2 |
| 3 |
| 2 |
②当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点.
解答: 解:(1)∵抛物线y=ax2+x+c的顶点为M(-1,-2),
解:(1)∵抛物线y=ax2+x+c的顶点为M(-1,-2),
∴该抛物线的解析式为y=a(x+1)2-2.
即:y=ax2+2ax+a-2.
∴2a=1.
解得 a=
.
故该抛物线的解析式是:y=
x2+x-
.
当y=0时,
x2+x-
=0.
解之得 x1=-3,x2=1.
∴B(-3,0),C(1,0);
(2)①证明:将抛物线y=
x2+x-
沿x轴翻折后的图象,即新图象,仍过点B、C,其顶点M′与点M关于x轴对称,则M′(-1,2).
设新抛物线的解析式为:y=a′(x+1)2+2.
∵y=a′(x+1)2+2过点C(1,0),
∴a′(1+1)2+2=0,
解得,a′=-
.
∴翻折后得到的新抛物线的解析式为:y=-
x2-x+
.
当-4x+6=
x2+x-
时,有:x2-6x+9=0,
解得,x1=x2=3,此时,y=-6.
∴新抛物线y=-
x2-x+
与直线l有唯一的交点N(3,-6);
②
≤t≤6.
附解答过程:
∵点N是新抛物线y=-
x2-x+
与直线l有唯一的交点,
∴直线l与新抛物线y=-
x2-x+
在x轴上方部分(即G)无交点,
∴当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点,
运动t秒时,点B的坐标为(-3+t,0),点C的坐标为(1+t,0),直线与x轴交点为(
,0).
∵当
=-3+t时,t=6
∴图象G与直线l有公共点时,
≤t≤6.
 解:(1)∵抛物线y=ax2+x+c的顶点为M(-1,-2),
解:(1)∵抛物线y=ax2+x+c的顶点为M(-1,-2),∴该抛物线的解析式为y=a(x+1)2-2.
即:y=ax2+2ax+a-2.
∴2a=1.
解得 a=
| 1 |
| 2 |
故该抛物线的解析式是:y=
| 1 |
| 2 |
| 3 |
| 2 |
当y=0时,
| 1 |
| 2 |
| 3 |
| 2 |
解之得 x1=-3,x2=1.
∴B(-3,0),C(1,0);
(2)①证明:将抛物线y=
| 1 |
| 2 |
| 3 |
| 2 |
设新抛物线的解析式为:y=a′(x+1)2+2.
∵y=a′(x+1)2+2过点C(1,0),
∴a′(1+1)2+2=0,
解得,a′=-
| 1 |
| 2 |
∴翻折后得到的新抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
当-4x+6=
| 1 |
| 2 |
| 3 |
| 2 |
解得,x1=x2=3,此时,y=-6.
∴新抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
②
| 2 |
| 3 |
附解答过程:
∵点N是新抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴直线l与新抛物线y=-
| 1 |
| 2 |
| 3 |
| 2 |
∴当直线l经过点C时产生第一个公共点,经过点B时是最后一个公共点,
运动t秒时,点B的坐标为(-3+t,0),点C的坐标为(1+t,0),直线与x轴交点为(
| 6+t |
| 4 |
∵当
| 6+t |
| 4 |
∴图象G与直线l有公共点时,
| 2 |
| 3 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和直线与抛物线的交点问题.在求有关于翻折变换的题目,一定要数形结合,这样可以使抽象的问题变得具体化,降低了解题的难度与梯度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 一个几何体的三视图如图,则根据已知的数据,可得这个几何体的侧面积是( )
一个几何体的三视图如图,则根据已知的数据,可得这个几何体的侧面积是( )| A、15π | B、24π |
| C、12π | D、20π |
 为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有
为了解今年春节时学生自由支配的压岁钱数目,某部门从全市初三年级150000名学生中随机抽取了10000学生进行调查,并将这部分学生自由支配的压岁钱数目绘制成频率分布直方图,请估计全市初三年级约有 解不等式2(x-1)+5<3x,并把解集在数轴上表示出来.
解不等式2(x-1)+5<3x,并把解集在数轴上表示出来.
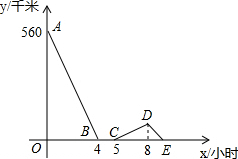 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: