Question

在Rt△ABC中，∠C=90°，AD平分∠CAB，AC=6，BC=8，CD=__________．

Answer 1

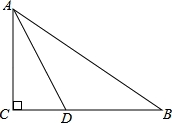
3．

【考点】角平分线的性质；勾股定理．

【分析】过点D作DE⊥AB于E，利用勾股定理列式求出AB，再根据角平分线上的点到角的两边距离相等可得CD=DE，然后根据△ABC的面积列式计算即可得解．

【解答】解：如图，过点D作DE⊥AB于E，

∵∠C=90°，AC=6，BC=8，

∴AB===10，

∵AD平分∠CAB，

∴CD=DE，

∴S_△ABC=AC•CD+AB•DE=AC•BC，

即×6•CD+×10•CD=×6×8，

解得CD=3．

故答案为：3．

【点评】本题考查了角平分线上的点到角的两边距离相等的性质，熟记性质并利用三角形的面积列出方程是解题的关键．