题目内容
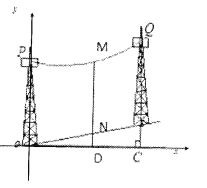
【题目】如图，在斜坡上按水平距离间隔50米架设电缆，塔柱上固定电缆的位置
，
离塔柱底部的距离均为20米.若以点
为原点，以水平地面
所在的直线为
轴，建立如图所示的坐标系，已知斜坡
所在直线的解析式为
，两端挂起的电缆下垂近似成二次项系数
为抛物线的形状.
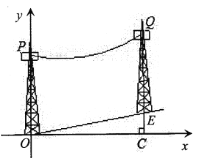
（1）点的坐标为 ，点的坐标为 ；
（2）求电缆近似成的抛物线的解析式；
（3）小明说：在抛物线顶点处，下垂的电缆在竖直方向上与斜坡的距离最近。你是否认同？请计算说明。
【答案】（1）
，
；（2）
；（3）不认同，见解析.
【解析】
（1）直接由题意即可得到答案.
（2）设抛物线的解析式为
，将点A（0，20），C（50，30）代入求解可得；
（3）先求得抛物线的顶点，设
为抛物线上一点，过点作
轴的垂线，交斜坡于点
，交轴一点
，列出
的解析式可得出MN最小值时x的值与抛物线顶点的比较.
解：(1)由题意易知P点坐标为（0，20），Q点坐标为（50，30）.
（2）设抛物线的函数解析式为
，
把和代入，得
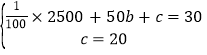
解得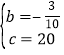
抛物线的函数解析式为
（3）不认同.
抛物线的顶点为
如图，设
为抛物线上一点，过点作
轴的垂线，交斜坡于点
，交轴一点
，
设点
，则为
当
时，
有最小值，此时下垂的电缆在竖直方向上斜坡的距离最近.
练习册系列答案
相关题目
