Question

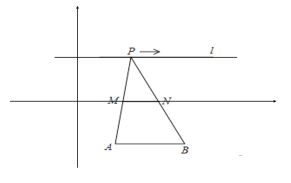
【题目】如图，在直角坐标系中，点，为定点，A（2，－3），B（4，－3），定直线，是上一动点，到AB的距离为6，，分别为，的中点，对下列各值：①线段的长度始终为1；②的周长固定不变；③的面积固定不变；④若存在点Q使得四边形APBQ是平行四边形，则Q到所在的直线的距离必为9；其中说法正确的是__（填序号）

Answer 1

【答案】①③④

【解析】

根据三角形的中位线定理可判断①；

根据、的长度随点的移动而变化可判断②；

根据的长度不变，点到的距离等于与的距离的一半并结合三角形的面积公式可判断③；

根据点Q到MN所在的直线的距离等于Q到AB的距离与AB、MN的距离之和可判断④.

解：∵点，为定点，AB=2，点，分别为，的中点，

∴是的中位线，∴ ，故①符合题意；

∵、的长度随点的移动而变化，

∴的周长会随点的移动而变化，故②不符合题意；

∵的长度不变，l∥MN，点到的距离等于与的距离的一半，

∴的面积不变，故③符合题意；

∵l到AB的距离为6，点M到AB的距离为3，则Q到MN所在的直线的距离等于Q到AB的距离与AB、MN的距离之和，即为9，故④符合题意；

综上所述，说法正确的是：①③④．