题目内容
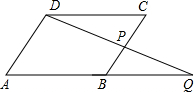
 已知,E为?ABCD边CD延长线上的一点,连接BE交AC于O,交AD于F,且OF=2,EF=3,则OB的长为________.
已知,E为?ABCD边CD延长线上的一点,连接BE交AC于O,交AD于F,且OF=2,EF=3,则OB的长为________.

分析:即证OB:OF=OE:OB.由AB∥CD得△AOB∽△COE,有OE:OB=OC:OA;由AD∥BC得△AOF∽△COB,有OB:OF=OC:OA,进而得出OB2=OF•OE,即可求出OB的长.
解答:证明:∵AB∥CD,
∴△AOB∽△COE.
∴OE:OB=OC:OA;
∵AD∥BC,
∴△AOF∽△COB.
∴OB:OF=OC:OA.
∴OB:OF=OE:OB,即
OB2=OF•OE.
∵OF=2,EF=3,
∴OB2=2×5=10,
∴OB=
 .
.故答案为:
 .
.点评:此题考查了相似三角形的判定和性质,综合性较强,有一定难度,证线段的乘积相等,通常转化为比例式形式,再证明所在的三角形相似,得出OB2=OF•OE是解决问题的关键.

练习册系列答案
相关题目
 如图,已知点E为?ABCD的BC边上的任意一点,则S△ADE:S□ABCD的值为( )
如图,已知点E为?ABCD的BC边上的任意一点,则S△ADE:S□ABCD的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|