题目内容
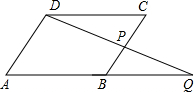
已知：P为?ABCD边BC上任意一点，DP交AB的延长线于Q点，求证：| BC |
| BP |
| AB |
| BQ |
分析：由于AB=CD，所以将
转化为
，再由平行线的性质可得
=
，进而求解即可．
| AB |
| BQ |
| CD |
| BQ |
| CD |
| BQ |
| PC |
| BP |
解答：证明：在平行四边形ABCD中，则AD∥BC，AB∥CD，
∴
=
=
∴
-
=
-
=
=1．
∴
| AB |
| BQ |
| CD |
| BQ |
| PC |
| BP |
∴
| BC |
| BP |
| AB |
| BQ |
| BC |
| BP |
| PC |
| BP |
| PB |
| BP |
点评：本题主要考查了平行四边形的性质以及相似三角形的判定及性质问题，能够熟练掌握．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
如图，已知点E为?ABCD的BC边上的任意一点，则S△ADE：S□ABCD的值为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
ABCD的对角线BD的中点，直线EF经过点O，分别交BA、DC的延长线于E、F两点，求证：AE＝CF．
