Question

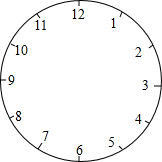
钟面上有1，2，3，…，11，12共十二个数字，如图所示．

(1)试在某些数的前面添加负号，使它们的代数和为零；

(2)能否改变钟面上的数，比如只剩下六个偶数，仍按第(1)小题的要求来做？

(3)请试着改变第(1)小题，使它更加有趣些，比如：哪些时间里分针和时针所夹的那些数的前面添加负号，钟面上的各数的代数和为零；

(4)在解上述各题的过程中，你能总结出一些什么数学规律？

Answer 1

答案：略
解析：

(1)∵39=12＋11＋10＋6=12＋11＋10＋5＋1=9＋11＋10＋5＋3＋1=…… ∴方案一：1＋2＋3＋4＋5－6＋7＋8＋9－10－11－12(本题答案不唯一，有124个之多，其余的由同学们自己完成)； (2)不可能； (3)∵39=4＋5＋6＋7＋8＋9=12＋11＋10＋1＋2＋3(这里将12，1视为连续自然数)， ∴当3:45～3:50或当9:15～9:20时，时针和分针所夹的那些数前面添加负号，钟面上所有数的代数和为零． (4)①正数的绝对值的和与负数的绝对值的和都等于39． ②如果将其一部分前面添加负号，代数和为零，那么将剩下的那些数前面添加负号，代数和也为零，如0－1＋2＋3＋4－5＋6＋7＋8＋9－10－11－12=0，则1－2－3－4＋5－6－7－8－9＋10＋11＋12=0． ③由于12＋11＋10=33＜39，因此必须再加上一个6才行，即将12，11，10，6前添加负号满足条件，所以添加负号的数至少要有四个；反之，最多不超过八个．

提示：

其余规律请同学们自己去发现、总结．