题目内容
在△ABC所在平面内,DE∥BC且分别交直线AB,AC于D,E,AD:AB=1:3,EC=12,则AE=________.
3或6
分析:分两种情况进行讨论:①D、E分别在AB、AC边上;②D、E分别在AB、AC边的反向延长线上.
解答: 解:设AE=x,分两种情况:
解:设AE=x,分两种情况:
①D、E分别在AB、AC边上,如图1;
∵DE∥BC,
∴ =
= =
= ,即
,即 =
= ,
,
解得x=6;
②D、E分别在AB、AC边的反向延长线上,如图2;
∵DE∥BC,
∴ =
= =
= ,
,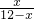 =
= ,
,
解得x=3.
综上可知AE的长为3或6.
故答案为3或6.
点评:本题考查了平行线分线段成比例定理:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.能够根据题意分情况进行讨论是解决本题的关键.
分析:分两种情况进行讨论:①D、E分别在AB、AC边上;②D、E分别在AB、AC边的反向延长线上.
解答:
 解:设AE=x,分两种情况:
解:设AE=x,分两种情况:①D、E分别在AB、AC边上,如图1;
∵DE∥BC,
∴
 =
= =
= ,即
,即 =
= ,
,解得x=6;
②D、E分别在AB、AC边的反向延长线上,如图2;
∵DE∥BC,
∴
 =
= =
= ,
,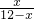 =
= ,
,解得x=3.
综上可知AE的长为3或6.
故答案为3或6.
点评:本题考查了平行线分线段成比例定理:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.能够根据题意分情况进行讨论是解决本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 12、如图,△ABC中,AB=AC,∠A=40°.在△ABC所在平面内,除了△ABC外,还有
12、如图,△ABC中,AB=AC,∠A=40°.在△ABC所在平面内,除了△ABC外,还有 如图.等腰三角形ABC(AB=AC≠BC)在△ABC所在平面内有一点P,且使得△ABP、△ACP、△BCP均为等腰三角形,则符合条件的点P共有( )个.
如图.等腰三角形ABC(AB=AC≠BC)在△ABC所在平面内有一点P,且使得△ABP、△ACP、△BCP均为等腰三角形,则符合条件的点P共有( )个.