题目内容
某水库大坝的横断面是梯形ABCD,坝顶宽CD=3米,斜坡AD=16米,坝高8m,斜坡BC的坡度为1:3,则斜坡AD的坡角∠A=分析:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,得到两个直角三角形和一个矩形,在Rt△BCF、Rt△AED中已知一边和一角,或两边的比,满足解直角三角形的条件,可求出CD和BD的长.
解答:解:过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形

∴CD=FE=3,CF=ED=8
∵sinA=ED:AD=8:16=1:2
∴∠A=30°,AE=EDcot30°=8
∵CF:BF=1:3
∴BF=3CF=24
即AB=BF+EF+AE=24+3+8
=(8
+27)米.

∴CD=FE=3,CF=ED=8
∵sinA=ED:AD=8:16=1:2
∴∠A=30°,AE=EDcot30°=8
| 3 |
∵CF:BF=1:3
∴BF=3CF=24
即AB=BF+EF+AE=24+3+8
| 3 |
| 3 |
点评:本题利用了构造直角三角形和矩形,利用锐角三角函数的概念和坡度的概念求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 31、如图,某水库大坝的横断面是等腰梯形,坝顶宽6米,坝高10米.斜坡AB的坡度为1:2(AR:BR).现要加高2米,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长为50米的大坝,需要多少土方.
31、如图,某水库大坝的横断面是等腰梯形,坝顶宽6米,坝高10米.斜坡AB的坡度为1:2(AR:BR).现要加高2米,在坝顶宽度和斜坡坡度均不变的情况下,加固一条长为50米的大坝,需要多少土方. 如图,某水库大坝的横断面是梯形,坝外斜坡的坡比i=l:1,两个坡角的和为75.,则坝内斜坡的坡比是
如图,某水库大坝的横断面是梯形,坝外斜坡的坡比i=l:1,两个坡角的和为75.,则坝内斜坡的坡比是 某水库大坝的横断面是一个梯形,如图,已知坝顶宽CD=3米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3.
某水库大坝的横断面是一个梯形,如图,已知坝顶宽CD=3米,斜坡AD=16米,坝高8米,斜坡BC的坡度i=1:3.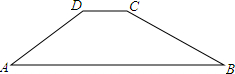 如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=
如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A= 如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.
如图所示,某水库大坝的横断面是梯形,坝顶宽CD=3m,坝高4m,背水坡的坡度是1:1.5,迎水坡的坡度是1:2.5,求坝底宽AB和坡角∠A.