题目内容
如图,在半径为2的中,B为圆周上一点,且B点坐标为(1, ),0A=4,将△AOB绕O点逆时针旋转60°后,则B点的对应点B1的坐标是( )
),0A=4,将△AOB绕O点逆时针旋转60°后,则B点的对应点B1的坐标是( )
A.(-
 ,
, )
)B.(-
 ,1)
,1)C.(-
 ,
, )
)D.(-1,
 )
)
【答案】分析:过B点作BC⊥y轴,垂足为C,由B(1, ),可知BC=1,OC=
),可知BC=1,OC= ,解直角三角形得∠BOC=30°,根据圆的对称性可知B关于y轴的对称点即为对应点B1.
,解直角三角形得∠BOC=30°,根据圆的对称性可知B关于y轴的对称点即为对应点B1.
解答: 解:如图,过B点作BC⊥y轴,垂足为C,
解:如图,过B点作BC⊥y轴,垂足为C,
由B(1, ),可知BC=1,OC=
),可知BC=1,OC= ,
,
在Rt△BOC中,tan∠BOC= =
= ,
,
∴∠BOC=30°,
延长BC交⊙O于B1点,
由圆的对称性可知∴∠B1OC=∠BOC=30°,
即∠B1OB=60°,
∴点B1与点B关于y轴对称,故B1(-1, ).
).
故选D.
点评:本题考查了旋转的性质,圆的对称性,解直角三角形的知识.关键是根据点B的坐标确定特殊三角形.
 ),可知BC=1,OC=
),可知BC=1,OC= ,解直角三角形得∠BOC=30°,根据圆的对称性可知B关于y轴的对称点即为对应点B1.
,解直角三角形得∠BOC=30°,根据圆的对称性可知B关于y轴的对称点即为对应点B1.解答:
 解:如图,过B点作BC⊥y轴,垂足为C,
解:如图,过B点作BC⊥y轴,垂足为C,由B(1,
 ),可知BC=1,OC=
),可知BC=1,OC= ,
,在Rt△BOC中,tan∠BOC=
 =
= ,
,∴∠BOC=30°,
延长BC交⊙O于B1点,
由圆的对称性可知∴∠B1OC=∠BOC=30°,
即∠B1OB=60°,
∴点B1与点B关于y轴对称,故B1(-1,
 ).
).故选D.
点评:本题考查了旋转的性质,圆的对称性,解直角三角形的知识.关键是根据点B的坐标确定特殊三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在半径为2的中,B为圆周上一点,且B点坐标为(1,
如图,在半径为2的中,B为圆周上一点,且B点坐标为(1,| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-1,
|
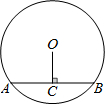 (2012•丹徒区模拟)如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是
(2012•丹徒区模拟)如图,在半径为5cm的⊙O中,圆心O到弦AB的距离为3cm,则弦AB的长是 如图,在半径为2的中,B为圆周上一点,且B点坐标为(1,
如图,在半径为2的中,B为圆周上一点,且B点坐标为(1, ),0A=4,将△AOB绕O点逆时针旋转60°后,则B点的对应点B1的坐标是
),0A=4,将△AOB绕O点逆时针旋转60°后,则B点的对应点B1的坐标是 ,
, )
) ,
, )
)



