题目内容
以O为圆心的两个同心圆的半径分别为 cm和
cm和 cm,⊙O1与这两个圆都相切,则⊙O1的半径是________;
cm,⊙O1与这两个圆都相切,则⊙O1的半径是________;
5或 cm
cm
分析:如果⊙O1与大圆内切,与小圆外切,则⊙O1的直径等于两半径的差.如果⊙O1与两圆都内切,⊙O1的直径等于两半径的和.可以求出⊙O1的半径.
解答:设⊙O1的半径为R,则
当⊙O1与大圆内切,与小圆外切时有:2R= -
- ,
,
解得:R=2 .
.
当⊙O1与两圆都内切时,有:2R= +
+ ,
,
解得:R=5.
故答案是:5或2 cm.
cm.
点评:本题考查的是圆与圆的位置关系,根据⊙O1与两同心相切,得到圆心距与两半径的关系,可以求出⊙O1的半径.
 cm
cm分析:如果⊙O1与大圆内切,与小圆外切,则⊙O1的直径等于两半径的差.如果⊙O1与两圆都内切,⊙O1的直径等于两半径的和.可以求出⊙O1的半径.
解答:设⊙O1的半径为R,则
当⊙O1与大圆内切,与小圆外切时有:2R=
 -
- ,
,解得:R=2
 .
.当⊙O1与两圆都内切时,有:2R=
 +
+ ,
,解得:R=5.
故答案是:5或2
 cm.
cm.点评:本题考查的是圆与圆的位置关系,根据⊙O1与两同心相切,得到圆心距与两半径的关系,可以求出⊙O1的半径.

练习册系列答案
相关题目
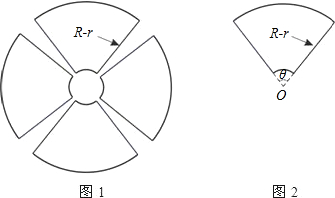 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;

 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径; 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;