题目内容
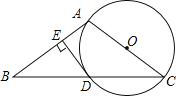
【题目】在等腰直角三角形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上(
上(![]() ),作
),作![]() ,且
,且![]() ,连接
,连接![]() ,如图(1).
,如图(1).
(1)求证:![]() ;
;
(2)延长![]() 至点
至点![]() ,使得
,使得![]() ,
,![]() 与
与![]() 交于点
交于点![]() .如图(2).
.如图(2).
①求证:![]() ;
;
②求证:![]() .
.

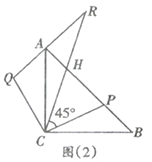
【答案】(1)见解析;(2)①见解析;②见解析
【解析】
(1)依据AC=BC,可得∠CAB=∠B=45°,依据AQ⊥AB,可得∠QAC=∠CAB=45°=∠B,即可得到△ACQ≌△BCP;
(2)①依据△ACQ≌△BCP,则∠QCA=∠PCB,依据∠RCP=45°,即可得出∠QCR=45°=∠QAC,根据∠Q为公共角,可得△CQR∽△AQC,即可得到CQ2=QAQR;
②判定△QCH≌△PCH(SAS),即可得到HQ=HP,在Rt△QAH中,QA2+AH2=HQ2,依据QA=PB,即可得到AH2+PB2=HP2.
(1)∵AC=BC,
∴∠CAB=∠B=45°,
又∵AQ⊥AB,
∴∠QAC=∠CAB=45°=∠B,
在△ACQ和△BCP中,
 ,
,
∴△ACQ≌△BCP(SAS);
(2)①由(1)知△ACQ≌△BCP,则∠QCA=∠PCB,
∵∠RCP=45°,
∴∠ACR+∠PCB=45°,
∴∠ACR+∠QCA=45°,即∠QCR=45°=∠QAC,
又∠Q为公共角,
∴△CQR∽△AQC,
∴![]() ,
,
∴CQ2=QAQR;
②如图,连接QH,

由(1)(2)题知:∠QCH=∠PCH=45°,CQ=CP.
又∵CH是△QCH和△PCH的公共边,
∴△QCH≌△PCH(SAS).
∴HQ=HP,
∵在Rt△QAH中,QA2+AH2=HQ2,
又由(1)知:QA=PB,
∴![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】借鉴我们已有研究函数的经验,探索函数![]() 的图像与性质,研究过程如下,请补充完整.
的图像与性质,研究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
|
|
| 10 |
| -2 | 1 |
| 1 | -2 | 3 | 10 |
|
其中,![]() _______,
_______,![]() =________;
=________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出函数图像;
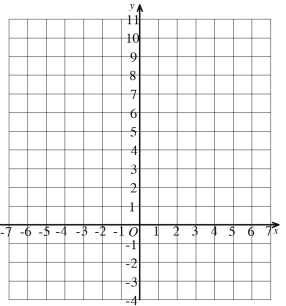
(3)观察函数图像:
①写出函数的一条图像性质:__________;
②当方程![]() 有且仅有两个不相等的实数根,根据函数图像直接写出
有且仅有两个不相等的实数根,根据函数图像直接写出![]() 的取值范围为________.
的取值范围为________.