Question

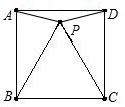
如图，已知P是正方形ABCD内一点，PA=1，PB=2，PC=3，以点B为旋转中心，将△ABP沿顺时针方向旋转，使点A与点C重合，这时P点旋转到M点。

【小题1】（1）请画出旋转后的图形，并说明此时△ABP以点B为旋转中心旋转了多少度？
【小题2】（2）求出PM的长度；
【小题3】（3）请你猜想△PMC的形状，并说明理由。

Answer 1

【小题1】（1）90º
【小题2】（2）
【小题3】（3）直角三角形

解析解：（1）旋转后的图形如下图：

由题意可知点A绕点B顺时针旋转了90度，在旋转前后大小和形状都没有发生变化，可知是图形绕点B顺时针旋转90度。
（2）是旋转得到的，选炸U你不改变图形的大小和形状
    
四边形ABCD是矩形

又

是直角三角形
在中，
由勾股定理
代入数据
(3) 在中：




是直角三角形