题目内容
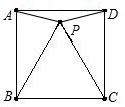 如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(
如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(A、
| ||||
B、
| ||||
| C、a | ||||
D、
|
分析:如图,设△PAD的外接圆为⊙O,根据已知条件可以证明△ABP≌△CDP,然后利用全等三角形的性质得到PA=PD,那么连接OP交AD与E点,根据垂径定理的推论知道E为AD的中点,并且OP⊥AD,根据已知条件和等边三角形的性质可以求出∠APD=150°,接着可以求出∠APO,再利用等腰三角形的性质可以求出∠AOE=30°,然后解直角三角形即可求解.
解答: 解:如图,设△PAD的外接圆为⊙O,
解:如图,设△PAD的外接圆为⊙O,
∵四边形ABCD是正方形,
∴AB=CD,
∵△PBC是等边三角形,
∴BP=CP=BC=AB=CD,∠PBC=∠PCB=60°,
∴∠ABP=∠PCD=30°,
∴∠APB=∠CPD=
=75°,
∴∠APD=360°-∠BPC-APB-∠CPD=360°-60°-75°-75°=150°,
连接OP交AD于E点,
根据垂径定理的推论知道E为AD的中点,并且OP⊥AD,
∴∠APO=75°
而OA=OP,
∴∠AOE=30°,
∴AE=
AO,
∴AD=AE=a,
∴正方形的边长为a.
故选C.
 解:如图,设△PAD的外接圆为⊙O,
解:如图,设△PAD的外接圆为⊙O,∵四边形ABCD是正方形,
∴AB=CD,
∵△PBC是等边三角形,
∴BP=CP=BC=AB=CD,∠PBC=∠PCB=60°,
∴∠ABP=∠PCD=30°,
∴∠APB=∠CPD=
| 180°-30° |
| 2 |
∴∠APD=360°-∠BPC-APB-∠CPD=360°-60°-75°-75°=150°,
连接OP交AD于E点,
根据垂径定理的推论知道E为AD的中点,并且OP⊥AD,
∴∠APO=75°
而OA=OP,
∴∠AOE=30°,
∴AE=
| 1 |
| 2 |
∴AD=AE=a,
∴正方形的边长为a.
故选C.
点评:此题既考查了正方形的性质、全等三角形的判定与性质、等边三角形的性质、也考查了垂径定理的推论、解直角三角形等知识点,综合性比较强,对于学生的能力要求比较高,平时加强训练.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是
15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.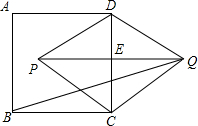 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为 如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,
如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,