Question

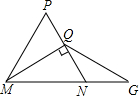
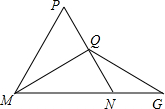
如图，⊿MNP中，∠P=60°,MN=MP,MQ⊥PN,垂足为Q,延长MN至G，取NG=NQ，若⊿MGP的周长为12，MQ=a，则⊿MGQ的周长是（    ）

A．8+2a             B．8+a              C．6+a              D．6+2a

 

Answer 1

【答案】

D

【解析】

试题分析：由∠P=60°，MN=NP可证得△MNP是等边三角形，再结合MQ⊥PN可得PM=PN=MN=4，NQ=NG=2，MQ=a，∠QMN=30°，∠PNM=60°，即可得到QG=MQ=a，由△MNP的周长为12，可得MN=4，NG=2，即可求得结果．

∵△MNP中，∠P=60°，MN=NP

∴△MNP是等边三角形．

又∵MQ⊥PN，垂足为Q

∴PM=PN=MN=4，NQ=NG=2，MQ=a，∠QMN=30°，∠PNM=60°

∵NG=NQ

∴∠G=∠QMN

∴QG=MQ=a，

∵△MNP的周长为12，

∴MN=4，NG=2，

∴△MGQ周长是6+2a．

考点：等边三角形的判定和性质

点评：等边三角形的判定和性质在初中数学中极为广泛，与各个知识点的结合极为容易，因而是中考的热点，在各种题型中均有出现，一般难度不大，需特别注意.