ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœΘ§≤ΔΆξ≥…œύ”Π»ΈΈώΘΚ
ΜΤΫπΖ÷Ην
ΧλΈΡ―ßΦ“ΩΣΤ’ά’Α―ΜΤΫπΖ÷Ην≥ΤΈΣ…ώ ΞΖ÷ΗνΘ§≤Δ÷Η≥ω±œ¥οΗγά≠ΥΙΕ®άμΘ®Ι¥Ι…Ε®άμΘ©ΚΆΜΤΫπΖ÷Ην «ΦΗΚΈ÷–ΒΡΥΪ±ΠΘ§«Α’ΏΚΟ±»ΜΤΫπΘ§Κσ’ΏΩΑ≥Τ÷ι±ΠΘ§άζ Ζ…œΉν‘γ’ΐ Ϋ‘Ύ ι÷– Ι”ΟΓΑΜΤΫπΖ÷ΗνΓ±’βΗωΟϊ≥ΤΒΡ «≈ΖΡΖΘ§19 άΦΆ“‘ΚσΓΑΜΤΫπΖ÷ΗνΓ±ΒΡΥΒΖ®÷πΫΞΝς––Τπά¥Θ§ΜΤΫπΖ÷Ην±ΜΙψΖΚ”Π”Ο”ΎΫ®÷ΰΒ»Νλ”ρΘ°ΜΤΫπΖ÷Ην÷ΗΑ―“ΜΧθœΏΕΈΖ÷ΈΣΝΫ≤ΩΖ÷Θ§ ΙΤδ÷–Ϋœ≥Λ≤ΩΖ÷”κœΏΕΈΉή≥Λ÷°±»Β»”ΎΫœΕΧ≤ΩΖ÷”κΫœ≥Λ≤ΩΖ÷÷°±»Θ§ΗΟ±»÷ΒΈΣ![]() Θ°”Οœ¬ΟφΒΡΖΫΖ®Θ®»γΆΦΔΌΘ©ΨΆΩ…“‘Ής≥ω“―÷ΣœΏΕΈ
Θ°”Οœ¬ΟφΒΡΖΫΖ®Θ®»γΆΦΔΌΘ©ΨΆΩ…“‘Ής≥ω“―÷ΣœΏΕΈ![]() ΒΡΜΤΫπΖ÷ΗνΒψ
ΒΡΜΤΫπΖ÷ΗνΒψ![]() ΘΚ
ΘΚ

ΔΌ“‘œΏΕΈ![]() ΈΣ±ΏΉς’ΐΖΫ–Έ
ΈΣ±ΏΉς’ΐΖΫ–Έ![]() Θ§
Θ§
ΔΎ»Γ![]() ΒΡ÷–Βψ
ΒΡ÷–Βψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§
Δέ―”≥Λ![]() ΒΫ
ΒΫ![]() Θ§ Ι
Θ§ Ι![]() Θ§
Θ§
Δή“‘œΏΕΈ![]() ΈΣ±ΏΉς’ΐΖΫ–Έ
ΈΣ±ΏΉς’ΐΖΫ–Έ![]() Θ§Βψ
Θ§Βψ![]() ΨΆ «œΏΕΈ
ΨΆ «œΏΕΈ![]() ΒΡΜΤΫπΖ÷ΗνΒψΘ°
ΒΡΜΤΫπΖ÷ΗνΒψΘ°
“‘œ¬ «÷ΛΟςΒψ![]() ΨΆ «œΏΕΈ
ΨΆ «œΏΕΈ![]() ΒΡΜΤΫπΖ÷ΗνΒψΒΡ≤ΩΖ÷Ιΐ≥ΧΘΚ
ΒΡΜΤΫπΖ÷ΗνΒψΒΡ≤ΩΖ÷Ιΐ≥ΧΘΚ
÷ΛΟςΘΚ…η’ΐΖΫ–Έ![]() ΒΡ±Ώ≥ΛΈΣ1Θ§‘ρ
ΒΡ±Ώ≥ΛΈΣ1Θ§‘ρ![]() Θ§
Θ§
![]() ΈΣ
ΈΣ![]() ÷–ΒψΘ§
÷–ΒψΘ§
![]() Θ§
Θ§
![]() ‘Ύ
‘Ύ![]() ÷–Θ§
÷–Θ§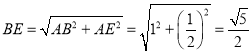 Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
Γ≠
»ΈΈώΘΚ
Θ®1Θ©≤Ι»ΪΧβ÷–ΒΡ÷ΛΟςΙΐ≥ΧΘΜ
Θ®2Θ©»γΆΦΔΎΘ§Βψ![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() ΒΡΜΤΫπΖ÷ΗνΒψΘ§Ζ÷±π“‘
ΒΡΜΤΫπΖ÷ΗνΒψΘ§Ζ÷±π“‘![]() ΈΣ±Ώ‘ΎœΏΕΈ
ΈΣ±Ώ‘ΎœΏΕΈ![]() Ά§≤ύΉς’ΐΖΫ–Έ
Ά§≤ύΉς’ΐΖΫ–Έ![]() ΚΆΨΊ–Έ
ΚΆΨΊ–Έ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°«σ÷ΛΘΚ
Θ°«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΔέΘ§‘Ύ’ΐΈε±Ώ–Έ![]() ÷–Θ§Ε‘Ϋ«œΏ
÷–Θ§Ε‘Ϋ«œΏ![]() ”κ
”κ![]() Ζ÷±πΫΜ”ΎΒψ
Ζ÷±πΫΜ”ΎΒψ![]() «σ÷ΛΘΚΒψ
«σ÷ΛΘΚΒψ![]() «
«![]() ΒΡΜΤΫπΖ÷ΗνΒψΘ°
ΒΡΜΤΫπΖ÷ΗνΒψΘ°
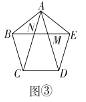
ΓΨ¥πΑΗΓΩΘ®1Θ©œξΦϊΫβΈωΘΜΘ®2Θ©œξΦϊΫβΈωΘΜΘ®3Θ©œξΦϊΫβΈω
ΓΨΫβΈωΓΩ
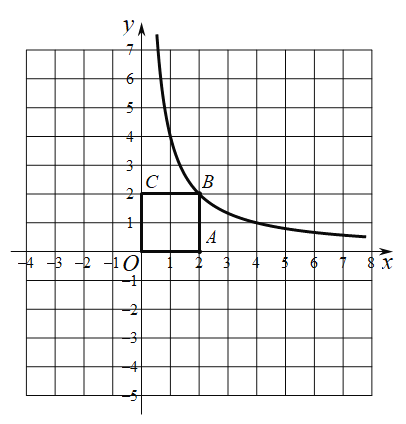
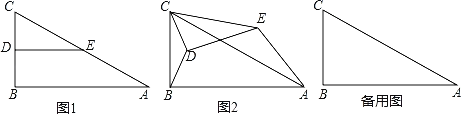
Θ®1Θ©…η’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ1Θ§‘ρAB=AD=1Θ§”…Ι¥Ι…Ε®άμΒΟ≥ω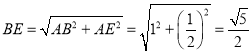 Θ§ΒΟ≥ω
Θ§ΒΟ≥ω![]() Θ§«σ≥ω
Θ§«σ≥ω![]() Θ§”…’ΐΖΫ–ΈΒΡ–‘÷ ΒΟ≥ω
Θ§”…’ΐΖΫ–ΈΒΡ–‘÷ ΒΟ≥ω![]() Θ§«σ≥ω
Θ§«σ≥ω![]() Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
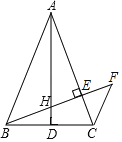
Θ®2Θ©”…’ΐΖΫ–ΈΚΆΨΊ–ΈΒΡ–‘÷ ΒΟ≥ωΓœEAB=ΓœBCD=90ΓψΘ§AC=CD=AE=DE=BFΘ§BC=DFΘ§”…ΒψCΈΣœΏΕΈABΒΡΜΤΫπΖ÷ΗνΒψΘ§ΒΟ≥ω![]() Θ§“ρ¥Υ
Θ§“ρ¥Υ![]() Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
Θ§Φ¥Ω…ΒΟ≥ωΫα¬έΘΜ
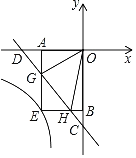
Θ®3Θ©ΗυΨί’ΐΈε±Ώ–ΈΒΡ–‘÷ ΒΟΒΫΓœDAE=ΓœDAEΘ§ΓœADE=ΓœAEM=36ΓψΘ§ΆΤ≥ωΓςAMEΓΉΓςAEDΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟΒΫΓύAEΘΚAD=AMΘΚAEΘ§ΒΟΒΫAE2=ADAMΘ§Β»ΝΩ¥ζΜΜΦ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ®1Θ©÷ΛΟςΘΚ…η’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ1Θ§‘ρAB=AD=1Θ§
ΓΏEΈΣAD÷–ΒψΘ§
ΓύAE=![]() Θ§
Θ§
Γύ‘ΎRtΓςBAE÷–Θ§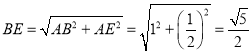
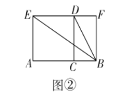
ΓΏEF=BE
Γύ![]()
Γύ![]() Θ§
Θ§
ΓΏΥΡ±Ώ–ΈAFGH «’ΐΖΫ–ΈΘ§
Γύ![]() Θ§
Θ§
Γύ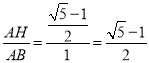 Θ§
Θ§
ΓύΒψH «œΏΕΈABΒΡΜΤΫπΖ÷ΗνΒψΘΜ
Θ®2Θ©÷ΛΟςΘΚΓΏΥΡ±Ώ–ΈACDE «’ΐΖΫ–ΈΘ§ΥΡ±Ώ–ΈCBFD «ΨΊ–ΈΘ§
ΓύΓœEAB=ΓœBCD=90ΓψΘ§AC=CD=AE=DE=BFΘ§BC=DFΘ§
ΓΏΒψCΈΣœΏΕΈABΒΡΜΤΫπΖ÷ΗνΒψΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύΓςEABΓΉΓςBCDΘΜ
Θ®3Θ©÷ΛΟςΘΚΓΏΈε±Ώ–ΈABCDE «’ΐΈε±Ώ–ΈΘ§
ΓύΓœBAE=ΓœAED=![]() Θ®5-2Θ©ΓΝ180Γψ=108ΓψΘ§AB=AE=DEΘ§
Θ®5-2Θ©ΓΝ180Γψ=108ΓψΘ§AB=AE=DEΘ§
ΓύΓœABE=ΓœAEM=ΓœDAE=ΓœADE=![]() Θ®180Γψ-108ΓψΘ©=36ΓψΘ§
Θ®180Γψ-108ΓψΘ©=36ΓψΘ§
ΓΏΓœDAE=ΓœDAEΘ§ΓœADE=ΓœAEM=36ΓψΘ§
ΓύΓςAMEΓΉΓςAEDΘ§
ΓύAEΘΚAD=AMΘΚAEΘ§
ΓύAE2=ADAMΘ§
ÿAE=DE=DMȧ/span>
ΓύDM2=ADAMΘ§
ΓύΒψM «ADΒΡΜΤΫπΖ÷ΗνΒψΘ°

 ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗ
ΜΣΕΪ Π¥σΑφ“ΜΩΈ“ΜΝΖœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥–ΘΨΌ––ΝΥΉ‘Ι± –¥¥Ϋ®»ΪΙζΈΡΟς≥« –÷Σ ΕΨΚ»ϋΜνΕ·Θ§≥θ“ΜΡξΦΕ»ΪΧεΆ§―ß≤ΈΦ”ΝΥ÷Σ ΕΨΚ»ϋΘ°
’Φ·ΫΧΨίΘΚœ÷ΥφΜζ≥ι»ΓΝΥ≥θ“ΜΡξΦΕ![]() ΟϊΆ§―ßΒΡΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±≥…Φ®Θ§Ζ÷ ΐ»γœ¬Θ®ΒΞΈΜΘΚΖ÷Θ©ΘΚ
ΟϊΆ§―ßΒΡΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±≥…Φ®Θ§Ζ÷ ΐ»γœ¬Θ®ΒΞΈΜΘΚΖ÷Θ©ΘΚ
’ϊάμΖ÷Έω ΐΨίΘΚ
≥…Φ® | ΤΒ ΐΘ®»Υ ΐΘ© |
|
|
|
|
|
|
|
|
Θ®1Θ©«κΫΪΆΦ±μ÷–Ω’»±ΒΡ≤ΩΖ÷≤Ι≥δΆξ’ϊΘΜ
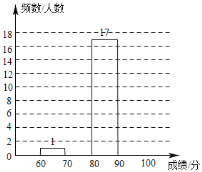
Θ®2Θ©―ß–ΘΨωΕ®±μ’ΟΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±≥…Φ®‘Ύ![]() Ζ÷ΦΑΤδ“‘…œΒΡΆ§―ßΘ°ΗυΨί…œΟφΆ≥ΦΤΫαΙϊΙάΦΤΗΟ–Θ≥θ“ΜΡξΦΕ
Ζ÷ΦΑΤδ“‘…œΒΡΆ§―ßΘ°ΗυΨί…œΟφΆ≥ΦΤΫαΙϊΙάΦΤΗΟ–Θ≥θ“ΜΡξΦΕ![]() »Υ÷–Θ§‘Φ”–Εύ…Ό»ΥΫΪΜώΒΟ±μ’ΟΘΜ
»Υ÷–Θ§‘Φ”–Εύ…Ό»ΥΫΪΜώΒΟ±μ’ΟΘΜ
Θ®3Θ©ΓΑ¥¥ΈΡ÷Σ ΕΨΚ»ϋΓ±÷–Θ§ ήΒΫ±μ’ΟΒΡ–ΓΚλΆ§―ßΒΟΒΫΝΥ”Γ”–Ι®…»ΓΔΦτ÷ΫΓΔ≤ ΒΤΓΔΩ÷ΝζΆΦΑΗΒΡΥΡΟΕΦΆΡν’¬Θ§Υΐ¥”÷–―Γ»ΓΝΫΟΕΥΆΗχΒήΒήΘ§‘ρ–ΓΚλΥΆΗχΒήΒήΒΡΝΫΟΕΦΆΡν’¬÷–Θ§«ΓΚΟ”–Ω÷ΝζΆΦΑΗΒΡΗ≈¬ «______________Θ°