题目内容
如图，△ABC内接于⊙O，且∠B = 60°．过点C作圆的切线l与直径AD的延长线交于点E，AF⊥l，垂足为F，CG⊥AD，垂足为G．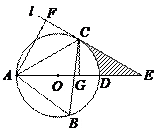
（1）求证：△ACF≌△ACG；
（2）若AF = 4
，求图中阴影部分的面积．
（1）略
（2）
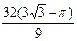
解析（1） 如图，连结CD，OC，则∠ADC =∠B = 60°．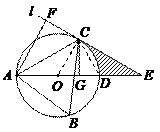
∵ AC⊥CD，CG⊥AD，∴∠ACG =∠ADC = 60°．
由于∠ODC = 60°，OC = OD，∴△OCD为正三角形，得∠DCO = 60°．
由OC⊥l，得∠ECD = 30°，∴∠ECG = 30° + 30° = 60°．
进而∠ACF = 180°－2×60° = 60°，∴ △ACF≌△ACG．
（2）在Rt△ACF中，∠ACF = 60°，AF = 4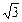
，得CF = 4．
在Rt△OCG中，∠COG = 60°，CG = CF = 4，得OC =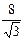
．
在Rt△CEO中，OE =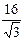
．
于是S阴影= S△CEO－S扇形COD=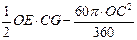
=．
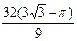练习册系列答案
相关题目
15、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC=4．BD为⊙O的直径，则BD=
21、如图，△ABC内接于⊙O，AB为⊙O的直径，点D在AB的延长线上，∠A=∠D=30°．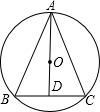
已知：如图，△ABC内接于⊙O，连接AO并延长交BC于点D，若AO=5，BC=8，∠ADB=90°，求△ABC的面积．
18、如图，△ABC内接于⊙O，∠A=30°，若BC=4cm，则⊙O的直径为（ ）
如图，△ABC内接于⊙O，AD⊥BC于点D，求证：∠BAD=∠CAO．