题目内容
【题目】如图，在
中，
，
，直角顶点
在
轴上，一锐角顶点
在
轴上．
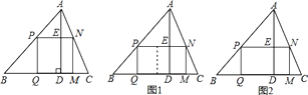
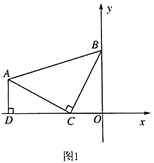
（1）如图1，若
垂直于轴，垂足为点
，点
的坐标是
，求点的坐标；
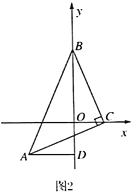
（2）如图2，直角边
在两坐标轴上滑动，过作
轴于．请猜想
、
、之间有怎样的关系，并证明你的猜想．
【答案】（1）
；（2）
，见解析
【解析】
（1）由题意可得AD=1，OD=3，由“AAS”可证△ACD≌△CBO可得AD=CO=1，BO=CD，即可求点B坐标；
（2）过点A作AE⊥x轴于E，可证四边形AEOD是矩形，可得AD=OE，由“AAS”可证△BOC≌△CEA，可得BO=CE，可得BO=CE=EO+OC=AD+OC．
解：（1）∵点
的坐标是
，∴
，
∵
∴
，
，
∴
，且
，
∴
∴
，
∴
∴点
坐标为
（2），
理由如下：如图，过点作
轴于
，
∵轴，
轴，
，
∴四边形
是矩形
∴
，
∵
∴
，
∴
，且
，
，
∴
∴
∴
练习册系列答案
相关题目
