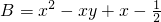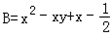Question

已知代数式（2x²+ax-y+6）-（2bx²-3x+5y-1）．
（1）当a=

-3

，b=

1

时，此代数式的值与字母x的取值无关；
（2）在（1）的条件下，多项式3（a²-2ab-b²）一（4a²+ab+b²）的值为

8

．

Answer 1

分析：（1）（2x²+ax-y+6）-（2bx²-3x+5y-1）=（2-2b）x²+（a+3）x-6y+7，与x无关即2-2b=0，a+3=0．
（2）先将整式化简为最简，再将a和b的值代入．

解答：解：（2x²+ax-y+6）-（2bx²-3x+5y-1）=（2-2b）x²+（a+3）x-6y+7，
又∵代数式的值与字母x的取值无关，
∴2-2b=0，a+3=0，
即：a=-3，b=1
（2）3（a²-2ab-b²）一（4a²+ab+b²）=-a²-7ab-4b²，
将a=-3，b=1代入可得：-a²-7ab-4b²=8．

点评：化简求值是课程标准中所规定的一个基本内容，它涉及对运算的理解以及运算技能的掌握两个方面，也是一个常考的题材．