题目内容
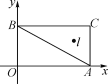
【题目】如图1,![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标
点坐标![]() 为且
为且![]() .
.
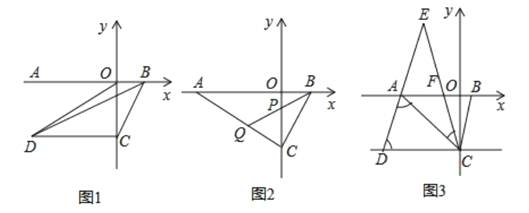
(1)求![]() 两点的坐标;
两点的坐标;
(2)求![]() ;
;
(3)如图2,若![]() 点坐标为
点坐标为![]() 点坐标为
点坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,
上一点,![]() 的延长线交线段
的延长线交线段![]() 于点
于点![]() ,若
,若![]() ,求出点
,求出点![]() 坐标.
坐标.
(4)如图3,若![]() ,点
,点![]() 在
在![]() 轴正半轴上任意运动,
轴正半轴上任意运动,![]() 的平分线
的平分线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 点的运动过程中,
点的运动过程中,![]() 的值是否发生变化,若不变化,求出比值;若变化请说明理由.
的值是否发生变化,若不变化,求出比值;若变化请说明理由.
【答案】(1)C(0,-2),D(-3,-2);(2)3;(3)Q(![]() ,
,![]() );(4)
);(4)![]() 值不变,且为
值不变,且为![]()
【解析】
(1)根据![]() 中绝对值和算术平方根的非负性可求得a和b的值,从而得到C和D的坐标;
中绝对值和算术平方根的非负性可求得a和b的值,从而得到C和D的坐标;
(2)求出CD的长度,再根据三角形的面积公式列式计算即可;
(3)根据![]() 可得△ABQ的面积等于△BOC的面积,求出△OBC的面积,再根据AB的长度可求得点Q的纵坐标,然后求出直线AC的表达式,代入点Q纵坐标即可求出点Q的横坐标;
可得△ABQ的面积等于△BOC的面积,求出△OBC的面积,再根据AB的长度可求得点Q的纵坐标,然后求出直线AC的表达式,代入点Q纵坐标即可求出点Q的横坐标;
(4)在△AOE和△BFC中,利用三角形内角和定理列式整理表示出∠ABC,然后相比即可得解.
解:(1)∵![]() ,
,
∴a+2=0,b+3=0,
∴a=-2,b=-3,
∴C(0,-2),D(-3,-2);
(2)∵C(0,-2),D(-3,-2),
∴CD=3,且CD∥x轴,
∴![]() =
=![]() ×3×2=3;
×3×2=3;
(3)∵![]() ,△OBP为公共部分,
,△OBP为公共部分,
∴S△ABQ=S△BOC,
∵B(2,0),C(0,-2)
∴S△BOC=![]() =2= S△ABQ,
=2= S△ABQ,
∵A(-3,0),
∴AB=5,
S△ABQ=![]() =2,
=2,
∴![]() ,
,
设直线AC的表达式为y=kx+b,
将A,C坐标代入,
![]() ,
,
解得: ,
,
∴直线AC的表达式为:![]() ,
,
令y=![]() ,
,
解得x=![]() ,
,
∴点Q的坐标为(![]() ,
,![]() );
);
(4)在△ACE中,设∠ADC=∠DAC=α,∠ACE=β,
∠E=∠DAC-∠ACE=α-β,
∵CE平分∠ACB,
∴∠BCE=∠ACE=β,
在△AFE和△BFC中,
∠E+∠EAF+∠AFE=180°,
∠ABC+∠BCF+∠BFC=180°,
∵CD∥x轴,
∴∠EAF=∠ADC=α,
又∵∠AFE=∠BFC,
∴∠E+∠EAF=∠ABC+∠BCF,
即α-β+α=∠ABC+β,
∴∠ABC=2(α-β),
∴![]() =
=![]() =
=![]() ,为定值.
,为定值.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案