题目内容
在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 于点
于点![]() .
.
(1)试说明:![]() ;
;
(2)求![]() 的值;
的值;
(3)求矩形![]() 的面积
的面积![]() .
.
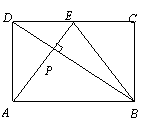 |
解:(1)
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
(2)当点![]() 为
为![]() 中点时,
中点时,![]()
∵四边形![]() 为矩形
为矩形![]()
∴![]()
∴![]() ,
,![]()
∴![]() ∽
∽![]()
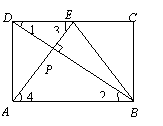
![]()
![]()
由![]() 可得
可得![]()
由(1)知![]()
在![]() 中,
中,![]()
![]()
(3)设AD=![]()
在![]() 中,
中,![]()
![]()
![]() ①
①
在![]() 中,
中,![]()
![]()
![]() ②
②
①、②联立可得![]()
由(2)知:![]()
![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,
中,![]() ,则有
,则有![]()
![]()
解得![]() (舍去负值)
(舍去负值)
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 于点
于点![]() .
.
(1)试说明:![]() ;
;
(2)求![]() 的值;
的值;
(3)求矩形![]() 的面积
的面积![]() .
.
 |
解:(1)
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]()
![]()
(2)当点![]() 为
为![]() 中点时,
中点时,![]()
∵四边形![]() 为矩形
为矩形![]()
∴![]()
∴![]() ,
,![]()
∴![]() ∽
∽![]()

![]()
![]()
由![]() 可得
可得![]()
由(1)知![]()
在![]() 中,
中,![]()
![]()
(3)设AD=![]()
在![]() 中,
中,![]()
![]()
![]() ①
①
在![]() 中,
中,![]()
![]()
![]() ②
②
①、②联立可得![]()
由(2)知:![]()
![]()
![]() ,
,![]()
![]()
![]()
在![]() 中,
中,![]() ,则有
,则有![]()
![]()
解得![]() (舍去负值)
(舍去负值)
![]()
![]()

 阅读快车系列答案
阅读快车系列答案