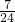Question

已知三角形三边之比是25：24：7，则最小角的余弦值是（　　）

• A、

  24

  25

• B、

  7

  25

• C、

  7

  24

• D、

  24

  7

Answer 1

分析：根据三角形三边的比可以判断三角形是直角三角形，则根据三角函数的定义就可以求解．

解答：解：已知三角形三边之比是25：24：7，
又∵7²+24²=25²，∴这个三角形是直角三角形．
则最小角即7所对的角，它的余弦值为

24

25

．
故选A．

点评：本题可以考查锐角三角函数的定义即运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比边．