题目内容
 如图,五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=1,则这个五边形ABCDE的面积等于
如图,五边形ABCDE中,∠ABC=∠AED=90°,AB=CD=AE=BC+DE=1,则这个五边形ABCDE的面积等于
- A.1
- B.2
- C.3
- D.4
A
分析:连接AC、AD,把三角形ADE绕A点逆时针旋转一个角度,使得AE与AB重合,D点旋转到D'点.易证得△ABD′≌△ABC,即△ADE≌△ABC,则两个三角形面积之和为 ,由△ACD≌△ACD′,S△ACD=
,由△ACD≌△ACD′,S△ACD= ,所以总面积为1.
,所以总面积为1.
解答: 解:连接AC、AD,
解:连接AC、AD,
∵∠ABC+∠ABD′=180°,
∴C、B、D′三点共线,
∴△ABD′≌△ABC,即△ADE≌△ABC,
∴S△ACD′= ×1×1=
×1×1= ,
,
∵△ACD′≌△ACD(SSS),
∴S△ACD= ,
,
∴这个五边形ABCDE的面积等于1,
故选A.
点评:本题考查了旋转的性质和全等三角形的判定和性质,是中档题,难度不大.
分析:连接AC、AD,把三角形ADE绕A点逆时针旋转一个角度,使得AE与AB重合,D点旋转到D'点.易证得△ABD′≌△ABC,即△ADE≌△ABC,则两个三角形面积之和为
 ,由△ACD≌△ACD′,S△ACD=
,由△ACD≌△ACD′,S△ACD= ,所以总面积为1.
,所以总面积为1.解答:
 解:连接AC、AD,
解:连接AC、AD,∵∠ABC+∠ABD′=180°,
∴C、B、D′三点共线,
∴△ABD′≌△ABC,即△ADE≌△ABC,
∴S△ACD′=
 ×1×1=
×1×1= ,
,∵△ACD′≌△ACD(SSS),

∴S△ACD=
 ,
,∴这个五边形ABCDE的面积等于1,
故选A.
点评:本题考查了旋转的性质和全等三角形的判定和性质,是中档题,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
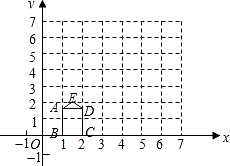 如图,矩形ABCD的长,宽分别为
如图,矩形ABCD的长,宽分别为
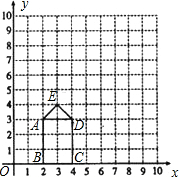 如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED.
如图,矩形ABCD的长、宽分别为3和2,OB=2,点E的坐标为(3,4)连接AE、ED. 如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见:
如图,四边形ABCD的内角和为2×180°=360°,五边形ABCDE的内角和为3×180°=540°,…由此可见: