题目内容
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的顶点.
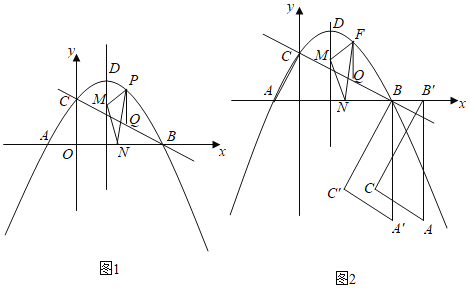
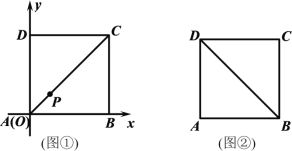
(1)如图1,P为直线BC上方抛物线上一动点,过点P作PQ∥y轴交BC于点Q.在抛物线的对称轴上有一动点M,在x轴上有一动点N,当6PQ﹣CQ的值最大时,求PM+MN+![]() NB的最小值;
NB的最小值;
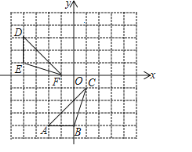
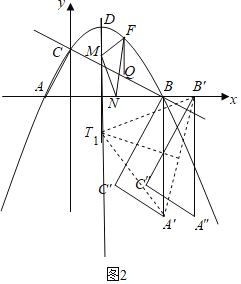
(2)如图2,将△ABC绕点B逆时针旋转90°后得到△A′BC',再将△A′BC′向右平移1个单位得到△A“B′C“,那么在抛物线的对称轴DM上,是否存在点T,使得△A′B′T为等腰三角形?若存在,求出点T到x轴的距离;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在.T到x轴的距离为
;(2)存在.T到x轴的距离为![]() 或4﹣
或4﹣![]() 或4+
或4+![]() 或2
或2![]() .
.
【解析】
(1)令x=0得到C(0,![]() ),令y=0得到A(﹣1,0),B(3,0),BC=2
),令y=0得到A(﹣1,0),B(3,0),BC=2![]() ,设直线BC解析式为y=kx+b,计算得到直线BC解析式为y=﹣
,设直线BC解析式为y=kx+b,计算得到直线BC解析式为y=﹣![]() x+
x+![]() ,设P(m,﹣
,设P(m,﹣![]() m2+
m2+![]() m+
m+![]() ),由题意得到BK=
),由题意得到BK=![]() ;过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,根据三角函数得到NT=
;过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,根据三角函数得到NT=![]() NB;由B(3,0),K(0,﹣
NB;由B(3,0),K(0,﹣![]() ),则直线BK解析式为y=
),则直线BK解析式为y=![]() x
x![]() ,根据平行线的性质及相似三角形的判定得到△P′WT∽△BKO,由相似三角形的性质结合题意进行计算,得到答案;
,根据平行线的性质及相似三角形的判定得到△P′WT∽△BKO,由相似三角形的性质结合题意进行计算,得到答案;
(2)由旋转的性质得到A′(3,﹣4),B′(4,0),设T(1,t),由于△A′B′T为等腰三角形,所以分三种情形:①A′T=B′T;②A′T=A′B′;③B′T=A′B′,进行计算,即可得到答案.
解:(1)在抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 中,令x=0,得y=
中,令x=0,得y=![]() ,∴C(0,
,∴C(0,![]() ),
),
令y=0,得0=﹣![]() x2+
x2+![]() x+
x+![]() ,解得x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),BC=2
,解得x1=﹣1,x2=3,∴A(﹣1,0),B(3,0),BC=2![]() ,
,
设直线BC解析式为y=kx+b,则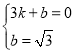 ,解得
,解得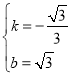 ,
,
∴直线BC解析式为y=﹣![]() x+
x+![]() ,
,
设P(m,﹣![]() m2+
m2+![]() m+
m+![]() ),则Q(m,﹣
),则Q(m,﹣![]() m+
m+![]() ),PQ=﹣
),PQ=﹣![]() m2+
m2+![]() m,CQ=
m,CQ=![]() m
m
∴6PQ﹣CQ=6(﹣![]() m2+
m2+![]() m)﹣
m)﹣![]() m=﹣2
m=﹣2![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∵﹣2![]() <0,∴当m=
<0,∴当m=![]() 时,6PQ﹣CQ的值最大,此时,P(
时,6PQ﹣CQ的值最大,此时,P(![]() ,
,![]() ),
),
由y=﹣![]() x2+
x2+![]() x+
x+![]() =-
=-![]() (x﹣1)2+
(x﹣1)2+![]() ,得抛物线对称轴为:x=1,
,得抛物线对称轴为:x=1,
作点P关于对称轴x=1的对称点P′(![]() ,
,![]() ),在y轴负半轴上取点K(0,﹣
),在y轴负半轴上取点K(0,﹣![]() ),连接BK交对称轴于S,则BK=
),连接BK交对称轴于S,则BK=![]() ,
,
过P′作P′T⊥BK于T,作P′W∥y轴交BK于点W,
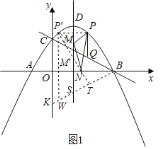
在△BNT中,![]() =tan∠OBK=
=tan∠OBK=![]() ,∴NT=
,∴NT=![]() NB,
NB,
∴线段P′T长度为PM+MN+![]() NB最小值,
NB最小值,
∵B(3,0),K(0,﹣![]() ),∴直线BK解析式为y=
),∴直线BK解析式为y=![]() x
x![]() ,
,
∴W(![]() ,
,![]() ),P′W=
),P′W=![]() ﹣(
﹣(![]() )=
)=![]() ,
,
∵P′W∥y轴,∴∠P′WT=∠BKO
∵∠P′TW=∠BOK=90°
∴△P′WT∽△BKO
∴![]() ,P′T=
,P′T=![]() ×
×![]() =
=![]() ,
,
∴PM+MN+![]() NB最小值=
NB最小值=![]() .
.
(2)存在.
∵△ABC绕点B逆时针旋转90°后得到△A′BC',再将△A′BC′向右平移1个单位得到△A′′B′C′′,
∴A′(3,﹣4),B′(4,0),∵点T在抛物线对称轴直线x=1上,∴设T(1,t)
∵△A′B′T为等腰三角形,∴分三种情形:
①A′T=B′T,(3﹣1)2+(﹣4﹣t)2=(4﹣1)2+(0﹣t)2,解得:t=![]() ,
,
∴此时T到x轴的距离为![]() ;
;
②A′T=A′B′,(3﹣1)2+(﹣4﹣t)2=(3﹣4)2+(﹣4﹣0)2,解得:t=﹣4+![]() 或﹣4﹣
或﹣4﹣![]() ,
,
∴此时T到x轴的距离为4﹣![]() 或4+
或4+![]() ;
;
③B′T=A′B′,(4﹣1)2+(0﹣t)2=(3﹣4)2+(﹣4﹣0)2,解得:t=2![]() 或﹣2
或﹣2![]() ,
,
∴此时T到x轴的距离为2![]() ;
;
综上所述,T到x轴的距离为![]() 或4﹣
或4﹣![]() 或4+
或4+![]() 或2
或2![]() .
.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
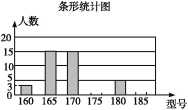
一线名师口算应用题天天练一本全系列答案【题目】甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:

根据以上信息,请解答下面的问题;
选手 | A平均数 | 中位数 | 众数 | 方差 |
甲 | a | 8 | 8 | c |
乙 | 7.5 | b | 6和9 | 2.65 |
(1)补全甲选手10次成绩频数分布图.
(2)a= ,b= ,c= .
(3)教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).