题目内容
如图，AC是矩形ABCD的对角线，AB=2，BC=
，点E、F分别是线段AB，AD上的点，连接CE，CF，当∠BCE=∠ACF，且CE=CF时，AE+AF=__
_
___.
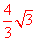18题解析：
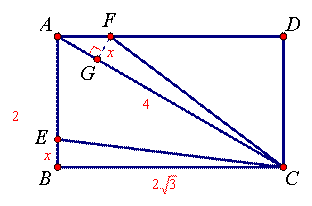
如图作FG⊥AC,易证△BCE≌△GCF（AAS），∴BE=GF,BC=CG，∵在Rt△ABC中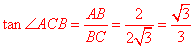
∴∠ACB=30°，∴AC=2AB=4，∠DAC=∠ACB=30°(内错角)，∵FG⊥AC，∴AF=2GF, ∴AE+AF=AE+2BE=AB+BE,
设BE=x，在Rt△AFG中AG=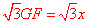
，
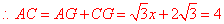，解得
∴AE+AF=AE+2BE=AB+BE=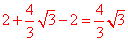
练习册系列答案
名校课堂系列答案
相关题目
≤
，并把它的解集在数轴上表示出来．
（2）在此次考试中，被抽取的获优秀成绩的有3人来自同一班级，这3人中有2男1女，该班班主任为让班上其他同学在练习跳绳的过程中效果更好，现打算从这3人中随机抽取2人到前排示范，请用画树状图或列表的方法求出所选同学是一男一女的概率. X 
∠ADC D．∠ADE＝
∠ADC