题目内容
如图，△ABC的三边的三等分点，A1、A2，B1、B2，C1、C2，连接A2B1、B2C1、C2A1，若△ABC周长为L，则六边形A1A2B1B2C1C2的周长为
- A.
L - B.
L - C.2L
- D.
L
A
分析：由这六个点为△ABC三边的三等分点，可得出三对相似三角形：△AB2C1∽△ABC，△BA1C2∽△BCA，△CA2B1∽△CBA；
再由相似三角形的性质可得
，
，
，
再由六边形的周长为B2C1+C1C2+A1C2+A1A2+A2B1+B1B2可得出六边形周长与三角形周长的关系，即可求得六边形周长．
解答：∵A1、A2、B1、B2、C1、C2为△ABC三边的三等分点
∴B2C1∥BC，A1C2∥AC，A2B1∥AB
∴△AB2C1∽△ABC，△BA1C2∽△BCA，△CA2B1∽△CBA
∴，，
∵六边形的周长为B2C1+C1C2+A1C2+A1A2+A2B1+B1B2=（AB+BC+AC）=L
故选A．
点评：本题考查了相似三角形的判定与性质．
分析：由这六个点为△ABC三边的三等分点，可得出三对相似三角形：△AB2C1∽△ABC，△BA1C2∽△BCA，△CA2B1∽△CBA；
再由相似三角形的性质可得
，，，再由六边形的周长为B2C1+C1C2+A1C2+A1A2+A2B1+B1B2可得出六边形周长与三角形周长的关系，即可求得六边形周长．
解答：∵A1、A2、B1、B2、C1、C2为△ABC三边的三等分点
∴B2C1∥BC，A1C2∥AC，A2B1∥AB
∴△AB2C1∽△ABC，△BA1C2∽△BCA，△CA2B1∽△CBA
∴
，，∵六边形的周长为B2C1+C1C2+A1C2+A1A2+A2B1+B1B2=
（AB+BC+AC）=L故选A．
点评：本题考查了相似三角形的判定与性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
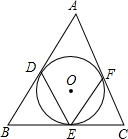如图，△ABC的三边分别切⊙O于D，E，F，若∠A=40°，则∠DEF=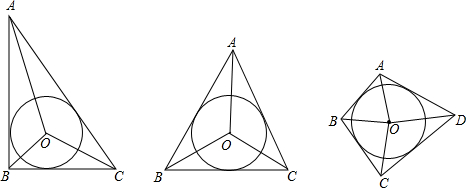
如图，△ABC的三边AB、BC、AC的长分别为4，6，8，其三条角平分线将△ABC分成三个三角形，则S△OAB：S△OBC：S△OAC=
如图，△ABC的三边长分别为AC=12，AB=15，BC=9．若将△ABC沿线段AD折叠，点C正好落在AB边上的点E处．求线段CD的长度．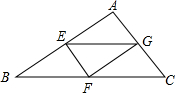
如图，△ABC的三边长分别是6cm、8cm、10cm，现在分别取三边的中点E、F、G，顺次连接E、F、G，则△EFG的面积为