题目内容
（2013•郑州模拟）现有形状、大小和颜色完全一样的三张卡片，上面分别标有数字“1”、“2”、“3”，第一次从这三张卡片中随机抽取一张，记下数字后放回，第二次再从这三张卡片中随机抽取一张并记下数字，则第二次抽取的数字大于第一次抽取的数字的概率是
．
| 1 |
| 3 |
| 1 |
| 3 |
分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与第二次抽取的数字大于第一次抽取的数字的情况，再利用概率公式求解即可求得答案．
解答：解：画树状图得：
∵共有9种等可能的结果，第二次抽取的数字大于第一次抽取的数字的有3种情况，
∴第二次抽取的数字大于第一次抽取的数字的概率是：
=
．
故答案为：
．
∵共有9种等可能的结果，第二次抽取的数字大于第一次抽取的数字的有3种情况，
∴第二次抽取的数字大于第一次抽取的数字的概率是：
| 3 |
| 9 |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
（2013•郑州模拟）已知：如图，CF平分∠DCE，点C在BD上，CE∥AB．若∠ECF=55°，则∠ABD的度数为（ ）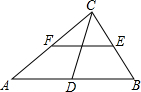
（2013•郑州模拟）如图，在Rt△ABC中，∠ACB=90°，D、E、F分别是AB、BC、CA的中点，若CD=5cm，则EF=