题目内容
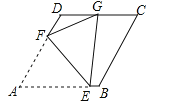
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= .
【答案】![]() .
.
【解析】
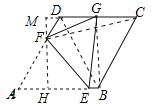
试题分析:延长CD,过点F作FM⊥CD于点M,连接GB、BD,作FH⊥AE交于点H,如图所示:
∵∠A=60°,四边形ABCD是菱形,∴∠MDF=60°,∴∠MFD=30°,设MD=x,则DF=2x,FM=![]() x,∵DG=1,∴MG=x+1,∴
x,∵DG=1,∴MG=x+1,∴![]() ,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=
,解得:x=0.3,∴DF=0.6,AF=1.4,∴AH=![]() AF=0.7,FH=AFsin∠A=1.4×
AF=0.7,FH=AFsin∠A=1.4×![]() =
=![]() ,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=
,∵CD=BC,∠C=60°,∴△DCB是等边三角形,∵G是CD的中点,∴BG⊥CD,∵BC=2,GC=1,∴BG=![]() ,设BE=y,则GE=2﹣y,∴
,设BE=y,则GE=2﹣y,∴![]() ,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF=
,解得:y=0.25,∴AE=1.75,∴EH=AE﹣AH=1.75﹣0.7=1.05,∴EF=![]() =
=![]() =
=![]() .故答案为:
.故答案为:![]() .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目