题目内容
如图，五边形ABCDE与五边形A′B′C′D′E′是位似图形，O为位似中心，OD=
OD′，则A′B′：AB为
- A.2：3
- B.3：2
- C.1：2
- D.2：1
D
分析：本题主要考查了位似变换的定义及作图，位似变换就是特殊的相似，且位似图形上任意一对对应点到位似中心的距离之比等于相似比，即对应边的比．
解答：位似图形上任意一对对应点，到位似中心的距离之比都等于相似比．
∴A′B′：AB=OD′：OD=2：1．
故选D．
点评：考查位似图形的性质．
分析：本题主要考查了位似变换的定义及作图，位似变换就是特殊的相似，且位似图形上任意一对对应点到位似中心的距离之比等于相似比，即对应边的比．
解答：位似图形上任意一对对应点，到位似中心的距离之比都等于相似比．
∴A′B′：AB=OD′：OD=2：1．
故选D．
点评：考查位似图形的性质．
练习册系列答案
相关题目
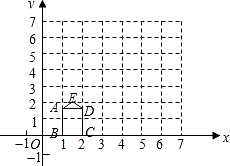如图，矩形ABCD的长，宽分别为
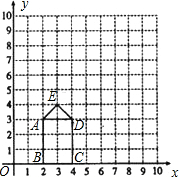如图，矩形ABCD的长、宽分别为3和2，OB=2，点E的坐标为（3，4）连接AE、ED．
如图，四边形ABCD的内角和为2×180°=360°，五边形ABCDE的内角和为3×180°=540°，…由此可见：