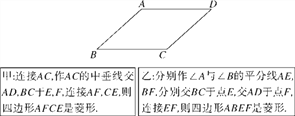
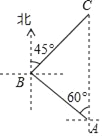
题目内容
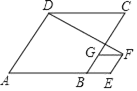
【题目】如图，菱形ABCD和菱形BEFG的边长分别是5和2，∠A＝60°，连结DF，则DF的长为_____．
【答案】
【解析】
延长FG交AD于点M，过点D作DH⊥AB交AB于点H，交GF的延长线于点N，由菱形的性质和勾股定理再结合已知条件可求出NF，DN的长，在直角三角形DNF中，再利用勾股定理即可求出DF的长．
延长FG交AD于点M，过点D作DH⊥AB交AB于点H，交GF的延长线于点N，
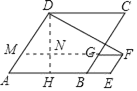
∵四边形ABCD和四边形BEFG都是菱形，
∴GF∥BE，EF∥AM，
∴四边形AMFE是平行四边形，
∴AM＝EF＝2，MF＝AE＝AB+BE＝5+2＝7，
∴DM＝AD﹣AM＝5﹣2＝3，
∵∠A＝60°，
∴∠DAH＝30°，
∴MN＝
DM＝
，
∴DN＝
＝
，NF＝MF﹣MN＝
，
在Rt△DNF中，DF＝
＝，
故答案为：．
练习册系列答案
相关题目
