题目内容
如图, 在长方形ABCD中,AB=3厘米.在CD边上找一点E,沿直线AE把△ABE折叠,若点D恰好落在BC边上点F处,且△ABF的面积是6平方厘米,则DE的长为( )

A.2cm B.3cm C.2.5cm D. cm
cm
【答案】
D
【解析】
试题分析:∵△ABF的面积是6cm2,AB=3cm,
∴BF=4cm.
在直角三角形ABF中,根据勾股定理,得
AF=5.根据折叠的性质,得AD=AF=5.
∵四边形ABCD是长方形,
∴BC=AD=5,
∴CF=5-4=1.
设DE=x,则EF=DE=x,CE=3-x,
在直角三角形EFC中,根据勾股定理,得
1+(3-x)2=x2,
解,得x= .
.
即DE= .
.
故选D
考点:翻折变换
点评:此题综合运用了矩形的性质、勾股定理以及折叠的性质,善于运用勾股定理构造方程求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,有一长方形纸片ABCD,AB=10,AD=6,将纸片折叠,使AD边落在AB边上,折痕为AE,再将△AED以DE为折痕向右折叠,AE与BC交于点F,则△CEF的面积与△ADE的面积的比为( )

| A、4:9 | B、2:3 | C、1:2 | D、2:5 |
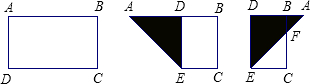
 如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为( )
如图,已知长方形纸片ABCD,AB=1.以点A所在直线为折痕折叠纸片,使点B落在AD上,折痕与BC交于点E;再以点E所在直线为折痕折叠纸片,使点A落在射线BC上,若折痕恰好经过点D,则长方形纸片ABCD的面积约为( )| A、1.4 | B、1.5 | C、1.6 | D、1.7 |
如图, 在长方形ABCD中,AB=3厘米.在CD边上找一点E,沿直线AE把△ABE折叠,若点D恰好落在BC边上点F处,且△ABF的面积是6平方厘米,则DE的长为( ) 
| A.2cm | B.3cm | C.2.5cm | D. cm cm |
 8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )
8、如图,已知长方形ABCD中AB=8 BC=10,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则DE的长为( )