题目内容
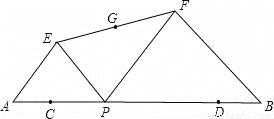
如图,已知AB=12,点C,D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )
①△EFP的外接圆的圆心为点G;②四边形AEFB的面积不变;
③EF的中点G移动的路径长为4;④△EFP的面积的最小值为8.
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题解析:如图,分别延长AE、BF交于点H. ∵等腰Rt△APE和等腰Rt△PBF, ∴, . ∴四边形EPFH为平行四边形, ∴EF与HP互相平分. ∵G为EF的中点, ∴G也为PH中点, 即在P的运动过程中,G始终为PH的中点, ∴G的运行轨迹为△HCD的中位线MN. ∵CD=12?2?2=8, ∴MN=4,即G的移...
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目


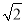 ,
, 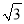 B. 5,12,13 C. 6,8,10 D.
B. 5,12,13 C. 6,8,10 D. 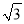 ,
, 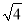 ,
, 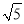
 B.
B.  C.
C.  D.
D. 

