题目内容
如图27228，在▱ABCD中，E是CD的延长线上一点，BE与AD交于点F，DE＝
CD.
(1)求证：△ABF∽△CEB；
(2)若△DEF的面积为2，求▱ABCD的面积．
图27228
(1)证明：∵AB∥CE，∴∠ABF＝∠E.
∵四边形ABCD为平行四边形，∠A＝∠C，
∴△ABF∽△CEB.
(2)解：∵DE＝CD，∴DE＝
EC.
由DF∥BC，得△EFD∽△EBC.
∴
＝
2＝
2＝
.
∴S△EBC＝9S△EFD＝9×2＝18.
S四边形BCDF＝S△EBC－S△EFD＝18－2＝16.
由AB∥DE，得△ABF∽△DEF.
∴
＝
2＝
.∴S△ABF＝4S△DEF＝4×2＝8.
∴S四边形ABCD＝S△ABF＋S四边形BCDF＝8＋16＝24.
练习册系列答案
阅读快车系列答案
相关题目
发展，有力地促进了
我省的经济建设，正在修建中的某段高速公路要招标，现有甲、乙两个工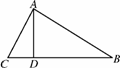
B．y＝
C．y＝
D．3xy＝2
(k＜0)的函数图象过点P(2，m)，Q(1，n)，则m与n的大小关系是：m____n (填“＞”“＝”或“＜”)．
（x＜0）的图象经过点A（﹣2，4）、B（m，2），过点A作AF⊥x轴于点F，过点B作BE⊥y轴于点E，交AF于点C，连接OA．
（2）若直线l过点O且平分△AFO的面积，求直线l的解析式．