题目内容
 如图△ABC中,BP平分∠B,CP平分∠C,若∠A=60°,则∠BPC=________度.
如图△ABC中,BP平分∠B,CP平分∠C,若∠A=60°,则∠BPC=________度.
120
分析:根据角平分线的定义得到∠1=∠2,∠3=∠4,根据三角形内角和定理得到∠1+∠2+∠3+∠4+∠A=180°,即2∠1+2∠3+∠A=180°,∠1+∠3+∠BPC=180°,经过代换得∴∠BPC=90°+ ∠A,然后把∠A=60°代入计算即可.
∠A,然后把∠A=60°代入计算即可.
解答: 解:如图,∵BP平分∠B,CP平分∠C,
解:如图,∵BP平分∠B,CP平分∠C,
∴∠1=∠2,∠3=∠4,
而∠1+∠2+∠3+∠4+∠A=180°,即2∠1+2∠3+∠A=180°,
又∵∠1+∠3+∠BPC=180°,
∴∠BPC=90°+ ∠A,
∠A,
而∠A=60°,
∴∠BPC=90°+30°=120°.
故答案为120.
点评:本题考查了三角形内角和定理:三角形的内角和为180°.也考查了角平分线的定义.
分析:根据角平分线的定义得到∠1=∠2,∠3=∠4,根据三角形内角和定理得到∠1+∠2+∠3+∠4+∠A=180°,即2∠1+2∠3+∠A=180°,∠1+∠3+∠BPC=180°,经过代换得∴∠BPC=90°+
 ∠A,然后把∠A=60°代入计算即可.
∠A,然后把∠A=60°代入计算即可.解答:
 解:如图,∵BP平分∠B,CP平分∠C,
解:如图,∵BP平分∠B,CP平分∠C,∴∠1=∠2,∠3=∠4,
而∠1+∠2+∠3+∠4+∠A=180°,即2∠1+2∠3+∠A=180°,
又∵∠1+∠3+∠BPC=180°,
∴∠BPC=90°+
 ∠A,
∠A,而∠A=60°,
∴∠BPC=90°+30°=120°.
故答案为120.
点评:本题考查了三角形内角和定理:三角形的内角和为180°.也考查了角平分线的定义.

练习册系列答案
相关题目
 如图△ABC中,BP平分∠B,CP平分∠C,若∠A=60°,则∠BPC=
如图△ABC中,BP平分∠B,CP平分∠C,若∠A=60°,则∠BPC= 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为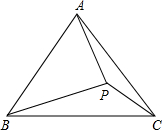 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为________.
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为________.