题目内容
一列数a1,a2,a3,…,其中 (n≥2,且n为整数),则a2012值为
(n≥2,且n为整数),则a2012值为
- A.

- B.2
- C.-1
- D.-

B
分析:由a1的值,及an= ,分别求出a2,a3,a4,a5的值,归纳总结得到数列的值以
,分别求出a2,a3,a4,a5的值,归纳总结得到数列的值以 ,2,-1循环,而2012除以3得到余数为2,即可确定出a2012的值.
,2,-1循环,而2012除以3得到余数为2,即可确定出a2012的值.
解答:∵a1= ,an=
,an= ,
,
∴a2= =2,a3=
=2,a3= =-1,a4=
=-1,a4=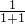 =
= ,a5=
,a5= =2,
=2,
∴数列a1,a2,a3,…an,以 ,2,-1循环,
,2,-1循环,
∵2012÷3=670…2,
∴a2012=2.
故选B.
点评:此题考查了规律型:数字的变化类,找出数列的值以 ,2,-1循环是解本题的关键.
,2,-1循环是解本题的关键.
分析:由a1的值,及an=
 ,分别求出a2,a3,a4,a5的值,归纳总结得到数列的值以
,分别求出a2,a3,a4,a5的值,归纳总结得到数列的值以 ,2,-1循环,而2012除以3得到余数为2,即可确定出a2012的值.
,2,-1循环,而2012除以3得到余数为2,即可确定出a2012的值.解答:∵a1=
 ,an=
,an= ,
,∴a2=
 =2,a3=
=2,a3= =-1,a4=
=-1,a4=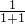 =
= ,a5=
,a5= =2,
=2,∴数列a1,a2,a3,…an,以
 ,2,-1循环,
,2,-1循环,∵2012÷3=670…2,
∴a2012=2.
故选B.
点评:此题考查了规律型:数字的变化类,找出数列的值以
 ,2,-1循环是解本题的关键.
,2,-1循环是解本题的关键. 
练习册系列答案
相关题目