Question

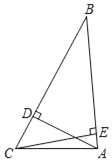
【题目】在锐角△ABC中，AD与CE分别是边BC与AB的高，AB＝12，BC＝16，S△ABC＝48，

求：(1)角B的度数；

(2)tanC的值．

Answer 1

【答案】(1)∠B＝30°；(2)tanC＝.

【解析】

（1）根据S△ABC＝48以及BC＝6,可求出AD的长度,然后由勾股定理可求出BD的长度,然后根据锐角三角函数的定义即可求出角B的度数,

（2）由于BC＝16,BD＝6,从而可知CD的长度,在Rt△ACD中,根据AD与CD的长度比即可求出tanc的值．

(1)由题意可知：S△ABC＝BCAD＝48,BC＝16,

∴AD＝6,

在Rt△ABD中,

AB＝12,

∴BD＝6,sinB＝＝,

∴∠B＝30°,

(2)∵BC＝16,BD＝6,

∴CD＝16﹣6,

在Rt△ACD中,

CD＝16﹣6,AD＝6,

∴tanC＝＝.