题目内容
 如图,RT△ABC中∠C=90°,BC=1cm,AB=2cm,把RT△ABC沿BC方向平移3cm至△DEF的位置,则图中的四边形ABFD的面积为
如图,RT△ABC中∠C=90°,BC=1cm,AB=2cm,把RT△ABC沿BC方向平移3cm至△DEF的位置,则图中的四边形ABFD的面积为
- A.
 cm2
cm2 - B.
 cm2
cm2 - C.
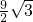 cm2
cm2 - D.
 cm2
cm2
A
分析:由题意可得S四边形ABFD的面积=S△ABC+S矩形ACFD,分别计算出其面积,即可解答.
解答:∵Rt△ABC中,∠C=90°,BC=1cm,AB=2cm,
∴AC= cm,
cm,
Rt△ABC沿BC方向平移3cm至△DEF的位置,
∴CF=3cm,
∴S四边形ABFD的面积=S△ABC+S矩形ACFD,
= ×1×
×1× +3×
+3× ,
,
= cm2.
cm2.
故选A.
点评:本题考查了平移的性质及勾股定理的应用,①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
分析:由题意可得S四边形ABFD的面积=S△ABC+S矩形ACFD,分别计算出其面积,即可解答.
解答:∵Rt△ABC中,∠C=90°,BC=1cm,AB=2cm,
∴AC=
 cm,
cm,Rt△ABC沿BC方向平移3cm至△DEF的位置,
∴CF=3cm,
∴S四边形ABFD的面积=S△ABC+S矩形ACFD,
=
 ×1×
×1× +3×
+3× ,
,=
 cm2.
cm2.故选A.
点评:本题考查了平移的性质及勾股定理的应用,①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.