ΧβΡΩΡΎ»ί
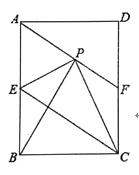
ΓΨΧβΡΩΓΩ‘ΎRtΓςABC÷–Θ§ΓœBAC=90ΓψΘ§BC=10Θ§tanΓœABC=![]() Θ§ΒψO «AB±Ώ…œΕ·ΒψΘ§“‘OΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΒΡΓ―O”κ±ΏBCΒΡΝμ“ΜΫΜΒψΈΣDΘ§ΙΐΒψDΉςABΒΡ¥ΙœΏΘ§ΫΜΓ―O”ΎΒψEΘ§ΝΣΫαBEΓΔAE
Θ§ΒψO «AB±Ώ…œΕ·ΒψΘ§“‘OΈΣ‘≤–ΡΘ§OBΈΣΑκΨΕΒΡΓ―O”κ±ΏBCΒΡΝμ“ΜΫΜΒψΈΣDΘ§ΙΐΒψDΉςABΒΡ¥ΙœΏΘ§ΫΜΓ―O”ΎΒψEΘ§ΝΣΫαBEΓΔAE
Θ®1Θ©»γΆΦΘ®1Θ©Θ§Β±AEΓΈBC ±Θ§«σΓ―OΒΡΑκΨΕ≥ΛΘΜ
Θ®2Θ©…ηBO=xΘ§AE=yΘ§«σyΙΊ”ΎxΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωΕ®“ε”ρΘΜ
Θ®3Θ©»τ“‘AΈΣ‘≤–ΡΒΡΓ―A”κΓ―O”–ΙΪΙ≤ΒψDΓΔEΘ§Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§«σDEΒΡ≥ΛΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©Γ―OΒΡΑκΨΕ≥ΛΈΣ![]() ΘΜΘ®2Θ©y =
ΘΜΘ®2Θ©y =![]() Θ§Ε®“ε”ρΘ®0ΘΦxΓή
Θ§Ε®“ε”ρΘ®0ΘΦxΓή![]() Θ©ΘΜΘ®3Θ©Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ
Θ©ΘΜΘ®3Θ©Β±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ![]() Μρ12Θ°
Μρ12Θ°
ΓΨΫβΈωΓΩ
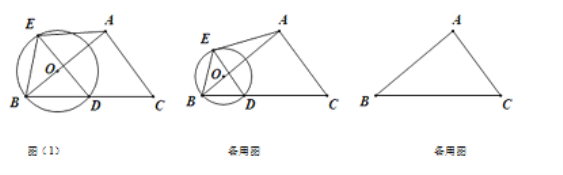
Θ®1Θ©»γΆΦ1÷–Θ§ΙΐΒψOΉςOGΓΆBD”ΎG…ηAB”κDEΒΡΫΜΒψΈΣFΘ° Ήœ»÷ΛΟςAEΘΫBDΘΫDCΘΫ10Θ§‘Όάϊ”Ο¥ΙΨΕΕ®άμ«σ≥ωBGΘ§‘ΎRtΓςBOD÷–Θ§Ϋβ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΘΜ
Θ®2Θ©»γΆΦ2÷–Θ§ΙΐΒψAΉςAHΓΆBC”ΎHΘ§»γΆΦΘ®2Θ©Θ§ Ήœ»«σ≥ωABΓΔACΓΔAHΘ§ΗυΨίyΘΫAEΘΫADΘΫ![]() Θ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ§Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΔΌ»τΒψD‘ΎHΒΡΉσ±ΏΘ§»γΆΦΘ®2Θ©Θ§ΔΎ»τΒψD‘ΎHΒΡ”“±ΏΘ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©ΙΐΒψOΉςOGΓΆBD”ΎGΘ§…ηAB”κDEΒΡΫΜΒψΈΣFΘ§»γΆΦΘ®1Θ©Θ§
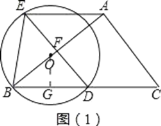
ΓΏOGΓΆBD”ΎGΘ§
ΓύBG=DGΘ°
ÿDEâABȧ
ΓύEF=DFΘ§
ÿAEøBCȧ
ΓύΓœAEF=ΓœBDFΘ°
‘ΎΓςAEFΚΆΓςBDF÷–Θ§
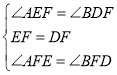 Θ§
Θ§
ΓύΓςAEFΓ’ΓςBDFΘ§
ΓύAE=BDΘ°
ΓΏΓœBFD=ΓœBAC=90ΓψΘ§
ΓύDEΓΈACΘ°
ÿAEøBCȧ
ΓύΥΡ±Ώ–ΈAEDC «ΤΫ––ΥΡ±Ώ–ΈΘ§
ΓύAE=DCΘ§
ΓύBD=DC=![]() BC=5Θ§
BC=5Θ§
ΓύBG=DG=![]() BD=
BD=![]() Θ°
Θ°
‘ΎRtΓςBGO÷–Θ§
tanΓœOBG=![]() =
=![]() Θ§
Θ§
ΓύOG=![]() BG=
BG=![]() ΓΝ
ΓΝ![]() =
=![]() Θ§
Θ§
ΓύOB=![]() =
=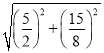 =
=![]() Θ§
Θ§
ΓύΓ―OΒΡΑκΨΕ≥ΛΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©ΙΐΒψAΉςAHΓΆBC”ΎHΘ§»γΆΦΘ®2Θ©Θ§
‘ΎRtΓςBAC÷–Θ§
tanΓœABC=![]() =
=![]() Θ§
Θ§
…ηAC=3kΘ§‘ρAB=4kΘ§
ΓύBC=5k=10Θ§
Γύk=2Θ§
ΓύAC=6Θ§AB=8Θ§
ΓύAH=![]() =
=![]() =
=![]() Θ§
Θ§
ΓύBH=![]() =
=![]() Θ§
Θ§
ΓύHC=BC©¹BH=10©¹![]() =
=![]() Θ°
Θ°
ÿABâDEȧ
ΓύΗυΨί¥ΙΨΕΕ®άμΩ…ΒΟDF=EFΘ§
ΓύAB¥Ι÷±ΤΫΖ÷DEΘ§
ΓύAE=ADΘ°
‘ΎRtΓςBGO÷–Θ§
tanΓœOBG=![]() =
=![]() Θ§
Θ§
ΓύOG=![]() BGΘ§
BGȧ
ΓύOB=![]() =
=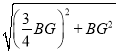 =
=![]() BG=xȧ
BG=xȧ
ΓύBG=![]() xΘ§
xȧ
ΓύBD=2BG=![]() xΘ§
xȧ
ΓύDH=BH©¹BD=![]() ©¹
©¹![]() xΘ§
xȧ
Γύy=AE=AD=![]() =
=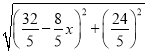 =
=![]()
Ε®“ε”ρΘ®0ΘΦxΓή![]() Θ©ΘΜ
Θ©ΘΜ
Θ®3Θ©ΔΌ»τΒψD‘ΎHΒΡΉσ±ΏΘ§»γΆΦΘ®2Θ©Θ§
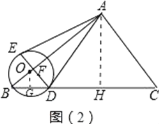
ÿAD=ACȧAHâDCȧ
ΓύDH=CH=![]() Θ§
Θ§
ΓύBD=BH©¹DH=![]() ©¹
©¹![]() =
=![]() Θ°
Θ°
‘ΎRtΓςBFD÷–Θ§
tanΓœFBD=![]() =
=![]() Θ§
Θ§
ΓύBF=![]() DFΘ§
DFȧ
ΓύBD=![]() =
=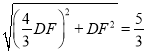 DF=
DF=![]() Θ§
Θ§
ΓύDF=![]() Θ§
Θ§
ΓύDE=2DF=![]() ΘΜ
ΘΜ
ΔΎ»τΒψD‘ΎHΒΡ”“±ΏΘ§
‘ρΒψD”κΒψC÷ΊΚœΘ§
ΓύBD=BC=10Θ§
Γύ![]() DF=10Θ§
DF=10Θ§
ΓύDF=6Θ§
ΓύDE=2DF=12Θ°
Ήέ…œΥυ ωΘΚΒ±Γ―A«ΓΚΟ“≤ΙΐΒψC ±Θ§DEΒΡ≥ΛΈΣ![]()