题目内容
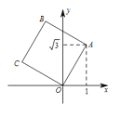
【题目】如图,已知直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
相交于点P.动点E从原点O出发,以每秒2个单位的速度沿着O→P→A的路线向点A匀速运动,同时动点F从原点O出发,以每秒2个单位的速度沿着射线OA的方向运动,当点E到达终点A时点F随即停止运动,设运动时间为t秒,当动点E、F所在的直线将△OPA的面积分成1∶2的两部分时,t的值为_________________。
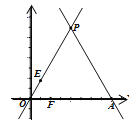
【答案】![]()
【解析】解:在![]() 中,令y=0,得:
中,令y=0,得: ![]() ,解得:x=4,∴OA=4.解方程组
,解得:x=4,∴OA=4.解方程组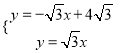 ,得:
,得: 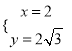 ,∴OP=
,∴OP=![]() =4,tan∠POA=
=4,tan∠POA=![]() ,∴∠POA=60°,∴△OPA是边长为4的等边三角形,
,∴∠POA=60°,∴△OPA是边长为4的等边三角形, ![]() .分两种情况讨论:
.分两种情况讨论:
①当E在OP上运动时,△OEF是边长为2t的等边三角形.∵△OEF∽△OPA,且面积比为1:3或2:3,∴ ![]() ,或
,或![]() ,解得:t=
,解得:t=![]() 或
或![]() .
.
②当E在PA上运动时,PE=2t-4,EA=8-2t,F(2t,0),E(t, ![]() ),直线EF为
),直线EF为![]() ,∴G(
,∴G(![]() ,
, ![]() ),∴OG=2×(
),∴OG=2×(![]() )=
)=![]() ,∴PG=
,∴PG=![]() =
=![]() .
.
∵![]() =
=![]() PGPE=
PGPE=![]() 或
或![]() ,解即:
,解即: ![]() 或
或![]() ,解得:t=
,解得:t=![]() 或
或![]() .
.

综上所述:t=![]() 或
或![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目