题目内容
22、如图：证明“三角形的内角和是180°”已知：
△ABC
求证：
∠A+∠B+∠C=180°
证明：过B点作直线EF∥AC．
分析：过点B作E∥FAC，由平行线的性质定理，即可推出∠EBA=∠A，∠FBC=∠C，然后根据平角的定义，等量代换，即可推出结论．
解答：证明：过点B作EF∥AC，
∴∠EBA=∠A，∠FBC=∠C，
∵∠EBA+∠ABC+∠FBC=180°，
∴∠A+∠C+∠ABC=180°，
∴三角形的内角和等于180°．
故答案为△ABC，∠A+∠B+∠C=180°．
∴∠EBA=∠A，∠FBC=∠C，
∵∠EBA+∠ABC+∠FBC=180°，
∴∠A+∠C+∠ABC=180°，
∴三角形的内角和等于180°．
故答案为△ABC，∠A+∠B+∠C=180°．
点评：本题主要考查三角形内角和定理，关键在于正确的做出辅助线，熟练运用平行线的性质定理．
练习册系列答案
相关题目
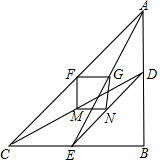两只大小不同的含45°角的三角板ABC和DBE如图摆放，直角顶点重合，连接AE，CD，F，M，N，G分别为线段AC，CD，ED，AE的中点．
如图：证明“三角形的内角和是180°”