题目内容
如图，在一个长方形花园ABCD中，若AB=a，AD=b，花园中建有一条长方形道路LMPQ及一条平行四边形道路RSKT，若LM=RS=c，则长方形花园中除道路外可绿化部分的面积为
- A.-bc+ab-ac+c2
- B.a2+ab+bc-ac
- C.bc-ab+ac+b2
- D.b2-bc+a2-ab
A
分析：求出矩形的面积等于ab，两条道路的面积分别为ac、bc，而重叠部分平行四边形的面积为c•c=c2，再根据可绿化面积等于矩形面积减去道路面积解答．
解答：S矩形ABCD=AB•AD=ab，
S道路面积=ca+cb-c2，
所以可绿化面积=S矩形ABCD-S道路面积
=ab-（ca+cb-c2），
=ab-ca-cb+c2．
故选A．
点评：本题主要考查矩形和平行四边形的面积的求解，道路重叠部分的面积的求解是解本题的关键，也是容易出错的地方．
分析：求出矩形的面积等于ab，两条道路的面积分别为ac、bc，而重叠部分平行四边形的面积为c•c=c2，再根据可绿化面积等于矩形面积减去道路面积解答．
解答：S矩形ABCD=AB•AD=ab，
S道路面积=ca+cb-c2，
所以可绿化面积=S矩形ABCD-S道路面积
=ab-（ca+cb-c2），
=ab-ca-cb+c2．
故选A．
点评：本题主要考查矩形和平行四边形的面积的求解，道路重叠部分的面积的求解是解本题的关键，也是容易出错的地方．
练习册系列答案
相关题目
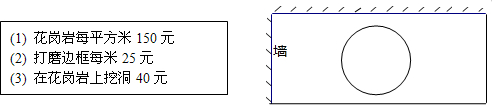
77、阅读材料后再解答问题
17、如图，一个长方形花坛中有一水沙子，要在四个梯形花池内分别和种红、黄、蓝三颜色的花（每个花池内只栽一种颜色的花），但相同颜色的花不许相邻，那么，共有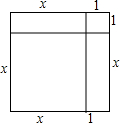
阅读材料后再解答问题