题目内容
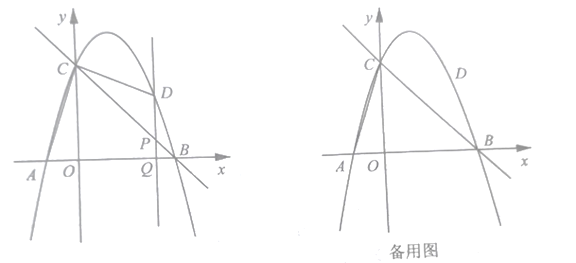
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一个动点(不与端点重合),
边上一个动点(不与端点重合),![]() 交
交![]() 于点
于点![]() 将
将![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() 当
当![]() 为等腰三角形时,则
为等腰三角形时,则![]() 的长为____.
的长为____.
【答案】2或![]()
【解析】
分两种情况讨论,作∠ABC的角平分线,根据三线合一的定理可以求出AC的长,再根据折叠的性质和勾股定理列方程,解方程即可求出AE的长.
解:在![]() 中,
中,
∵![]() ,
,
∴![]() 为等腰三角形,
为等腰三角形,
∴![]() .
.
分两种情况讨论,
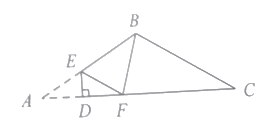
①作∠ABC的角平分线交AC于点O,如图1所示,
∵![]() 为等腰三角形,
为等腰三角形,
∴BO⊥AC,
∴![]() .
.
在Rt△OBC中,由勾股定理得:![]() ,
,
∴![]() ,
,
∵![]() 为等腰三角形,
为等腰三角形,
∴![]() ,
,
∴![]() ,
,
根据折叠的性质可知,![]() ,
,
∴![]() .
.
∵![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,
在Rt△AED中,设![]() ,则
,则![]() ,
,
根据勾股定理得,![]() ,
,
即 ,解得:
,解得:![]() ,
,
则![]()
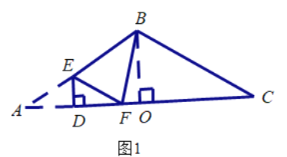
②作∠ABC的角平分线交AC于点O,作∠BFC的角平分线交BC于G,如图2所示,
∵![]() 为等腰三角形,
为等腰三角形,
∴BO⊥AC,
∴![]() .
.
在Rt△OBC中,由勾股定理得:![]() ,
,
∴![]() ,
,
∵![]() 为等腰三角形,
为等腰三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在Rt△CFG中,设![]() ,则
,则![]() .
.
由勾股定理得![]() ,
,
即![]() ,解得:
,解得:![]() ,
,
∴![]() ,
,
∴![]() .
.
根据折叠的性质可知,![]() ,
,
∴![]() .
.
∵![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,
在Rt△AED中,设![]() ,则
,则![]() ,
,
由勾股定理得![]() ,
,
即![]() ,解得
,解得![]() ,
,
∴![]() .
.
故答案为2或![]() .
.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目