题目内容
已知|a-3|+(b+1)2=0,求代数式b-a的值.
考点:代数式求值,非负数的性质:绝对值,非负数的性质:偶次方
专题:
分析:由于(b+1)2≥0,|a-3|≥0,而|a-3|+(b+1)2=0,由此即可得到a-3=0,b+1=0,接着可以求出a、b的值,然后代入所求代数式即可求出结果.
解答:解:∵(b+1)2≥0,|a-3|≥0,而|a-3|+(b+1)2=0,
∴a-3=0,b+1=0,
∴a=3且b=-1.
∴b-a=-1-3=-4.
∴a-3=0,b+1=0,
∴a=3且b=-1.
∴b-a=-1-3=-4.
点评:此题考查了非负数的性质,首先根据非负数的性质确定待定的字母的取值,然后代入所求代数式计算即可解决问题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
下列说法中,正确的是( )
| A、一个锐角的余角比这个角大 |
| B、一个锐角的补角比这个角大 |
| C、一个锐角的余角比这个角小 |
| D、一个钝角的补角比这个角大 |
设a,b互为相反数,c,d互为倒数,则2014a+
+2014b的值是( )
| 1 |
| 3cd |
| A、0 | ||
B、
| ||
C、-
| ||
| D、2014 |
计算
+
+
的结果是( )
| 1 |
| x-2 |
| 2 |
| x+2 |
| 4 |
| 4-x2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于多项式-2x2+3x-1,下列说法正确的是( )
| A、它是三次三项式 |
| B、它的二次项系数是2 |
| C、它的常数项是1 |
| D、它的一次项系数是3 |
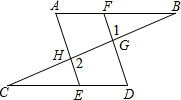 填写下列解题过程中的推理根据:
填写下列解题过程中的推理根据: