题目内容
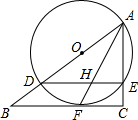如图，在Rt△ABC中，∠C=90°，点D是AB上一点，以AD为直径作⊙O交AC于E，与BC相切于点F，连接AF．（1）求证：∠BAF=∠CAF；
（2）若AC=6，BC=8，求BD和CE的长；
（3）若AF与DE交于H，求
| FH |
| FA |
考点：切线的性质,相似三角形的判定与性质
专题：
分析：（1）连结OF，运用内错角相等和等边对等角证明．
（2）作FM⊥AB于点M，得出△AMF≌△ACF，求出BM，再运用△BMF∽△BCA，得出BF=5，再运用切割定理求解．
（3）运用平行线的性质列出比例式求解．
（2）作FM⊥AB于点M，得出△AMF≌△ACF，求出BM，再运用△BMF∽△BCA，得出BF=5，再运用切割定理求解．
（3）运用平行线的性质列出比例式求解．
解答：
证明：（1）如图连结OF，
∵BC与⊙O相切于点F，
∴OFB=90°，
又∵∠C=90°，
∴OF∥AC，
∴∠OFA=∠CAF，
∵OF=OA，
∴∠OFA=∠BAF，
∴∠BAF=∠CAF；
（2）如图作FM⊥AB于点M，
∵∠BAF=∠CAF，∠C=∠AMF=90°
∴FM=FC，
在△AMF和△ACF中，
，
∴△AMF≌△ACF（AAS），
∴AM=AC=6，
∵AC=6，BC=8，
∴AB=
=
=10，
∴BM=10-6=4，
∵∠ABC=∠CBA，∠C=∠AMF，
∴△BMF∽△BCA，
∴
=
∴
=
∴BF=5，
∵BF2=BD•BA
∴52=BD×10
∴BD=
，
∵CF=BC-BF=8-5=3，
∵CF2=CE•CA，
∴CE=CF2÷CA=9÷6=
；
（3）∵HE∥FC，
∴
=
，
∴
=
，
∴
=
=4，
∴
=
，
故答案为：
．
证明：（1）如图连结OF，∵BC与⊙O相切于点F，
∴OFB=90°，
又∵∠C=90°，
∴OF∥AC，
∴∠OFA=∠CAF，
∵OF=OA，
∴∠OFA=∠BAF，
∴∠BAF=∠CAF；
（2）如图作FM⊥AB于点M，
∵∠BAF=∠CAF，∠C=∠AMF=90°∴FM=FC，
在△AMF和△ACF中，
|
∴△AMF≌△ACF（AAS），
∴AM=AC=6，
∵AC=6，BC=8，
∴AB=
| AC2+BC2 |
| 62+82 |
∴BM=10-6=4，
∵∠ABC=∠CBA，∠C=∠AMF，
∴△BMF∽△BCA，
∴
| BM |
| BC |
| BF |
| AB |
∴
| 4 |
| 8 |
| BF |
| 10 |
∴BF=5，
∵BF2=BD•BA
∴52=BD×10
∴BD=
| 5 |
| 2 |
∵CF=BC-BF=8-5=3，
∵CF2=CE•CA，
∴CE=CF2÷CA=9÷6=
| 3 |
| 2 |
（3）∵HE∥FC，
∴
| AH |
| FH |
| EA |
| CE |
∴
| AH+FH |
| FH |
| EA+CE |
| CE |
∴
| AF |
| FH |
| AC |
| CE |
∴
| FH |
| FA |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题主要考查切线的性质，全等三角形的判定和性质，相似三角形的判定和性质，平行线的性质等，解决本题的关键是运用三角形的全等和相似求出线段．
练习册系列答案
相关题目
下列现象：①电梯的升降运动，②飞机在地面上沿直线滑行，③风车的转动，④冷水加热过程中气泡的上升．其中属于平移的是（ ）
| A、①② | B、①③ | C、②③ | D、③④ |
如图，已知在△ABC中，AD是BC边上的中线，以AB为直径的⊙O交BC于点D，过D作MN⊥AC于点M，交AB的延长线于点N，过点B作BG⊥MN于G．
已知一次函数y1=x+m的图象与反比例函数
如图，点A、B分别在x，y轴上，点D在第一象限内，DC⊥x轴于点C，AO=CD=2，AB=DA=