Question

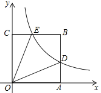
【题目】如图，已知抛物线与轴交于点、，顶点为M．

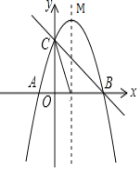
（1）求抛物线的解析式和点M的坐标；

（2）点E是抛物线段BC上的一个动点，设的面积为S，求出S的最大值，并求出此时点E的坐标；

（3）在抛物线的对称轴上是否存在点P，使得以A、P、C为顶点的三角形是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1），M(1，4)；（2）当时，S最大=，E(，)；（3）存在，P1(1，)，P2(1，)，P3(1，1)，P4(1，2)．

【解析】

（1）将点、的坐标代入函数解析式，列出方程组，通过解方程组求得、的值即可；利用配方法将函数解析式转化为顶点式，即可得到点的坐标；

（2）利用待定系数法确定直线解析式，由函数图象上点的坐标特征求得点、的坐标，然后根据两点间的距离公式求得长度，结合三角形的面积公式列出函数式，根据二次函数最值的求法求得点的横坐标，易得其纵坐标，则点的坐标迎刃而解了；

（3）需要分类讨论：点、、分别为直角顶点，利用勾股定理求得答案．

解：（1）抛物线与轴交于点、，

．

解得．

，则；

（2）如图，作轴交于点

，，

直线解析式为：．

设，则．

．

．

当时，S最大．

此时，点的坐标是，；

（3）设，、，

，，．

①当时，，即．解得．

②当时，，即．解得．

③当时，，即．解得或2．

综上所述，存在，符合条件的点的坐标是或或或，