题目内容
已知△ABC是腰长为1的等腰直角三角形,以等腰直角三角形ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以等腰直角三角形ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,依此类推,则第n个等腰直角三角形的斜边长为________.

答案:2n+2
分析 先求出第一个到第四个的等腰直角三角形的斜边的长,探究规律后即可解决问题.
解答 解:第一个等腰直角三角形的斜边为,
第二个等腰直角三角形的斜边为2=()2,
第三个等腰直角三角形的斜边为2=()3,
第四个等腰直角三角形的斜边为4=()4,
…
第n个等腰直角三角形的斜边为()n=2n+2.
故答案为2n+2.
点评 本题考查等腰直角三角形的有关知识、勾股定理、规律探究等知识,解题的关键是掌握从特殊得一般探究规律题目的方法,利用规律解决问题.属于中考常考题型.

练习册系列答案
相关题目
 已知△ABC是腰长为1的等腰直角三角形,以△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,第7个等腰直角三角形的腰长是
已知△ABC是腰长为1的等腰直角三角形,以△ABC的斜边AC为直角边,画第二个等腰直角三角形ACD,再以△ACD的斜边AD为直角边,画第三个等腰直角三角形ADE,…,依此类推,第7个等腰直角三角形的腰长是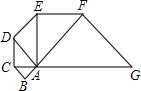 (2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是
(2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是
