题目内容
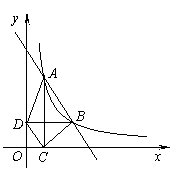
如图,在直角坐标平面内,函数![]() (x>0,m是常数)的图像经过A(1,4)、B(a,b),其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,DC
(x>0,m是常数)的图像经过A(1,4)、B(a,b),其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,DC![]() ,CB。
,CB。
(1)若△ABD的面积为4,求点B的坐标;
(2)求证:DC∥AB;(3)当AD=BC时,求直线AB的函数解析式。
 |
(1)解:∵函数![]() (x>0,m是常数)图像经过A(1,4),∴m=4
(x>0,m是常数)图像经过A(1,4),∴m=4
设BD、AC交于点E,据题意可得B(a,![]() ),D(0,
),D(0,![]() ),E(1,
),E(1,![]() ).
).
∵a>1,DB=a,AE=4-![]() ,由△ABD的面积为4,即
,由△ABD的面积为4,即![]()
得a=3,∴点B的坐标为(3,![]() )
)
(2)证明:据题意,点C的坐标为(1,0),DE=1,
∵a>1,易得EC=![]() ,BE=a-1. ∴
,BE=a-1. ∴![]() ,
,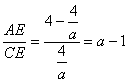
∴![]() ,∴DC∥AB
,∴DC∥AB
(3)解:∵DC∥AB,∴当AD=BC时,有两种情况:
①当AD∥BC时,四边形ADCB是平行![]() 四边形,由(2)得,
四边形,由(2)得,![]() ,
,
∴a-1=1,得a=2,∴点![]() B的坐标为(2,2)。
B的坐标为(2,2)。
设直线AB的函数解析式为为y=kx+b,则![]() 解得
解得![]()
∴直线AB的函数解析式是y=-2x+6。
②当AD与BC所在直线不平行时,四边形ADCB是等腰梯形,则BD=AC,
∴a=4,∴点B的坐标是(4,1)
设直线AB的函数解析式为y=kx+b,则![]() 解得
解得![]()
∴直线AB的函数解析式是y=-x+5.
综上所述,所求直线AB的函数解析式是y![]() =-2x+6或y=-x+5.
=-2x+6或y=-x+5.

练习册系列答案
相关题目
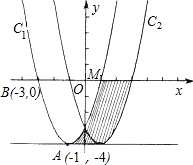 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)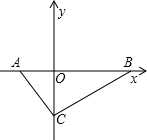 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=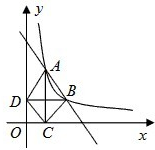 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是