题目内容
面积为18的圆内接四边形ABCD的对角线AC是直径,AD=DC,DE⊥AB于E,则DE= .
【答案】分析:连接BD,发现等腰直角三角形ACD和BDE.设⊙O的半径为R,DE=x,首先根据AC把四边形ABCD分割成的两个三角形的面积进行计算,求得AB+BC=6 ,再根据DE把四边形ABCD分割成的两部分的面积进行计算,即可求解.
,再根据DE把四边形ABCD分割成的两部分的面积进行计算,即可求解.
解答: 解:如图,连接BD,
解:如图,连接BD,
因为AC是直径,
所以∠ADC=90°.
因为AD=DC,
所以∠ACD=45°,
所以∠ABD=45°,又∠DEB=90°,
所以△DEB为等腰直角三角形,
所以DE=BE.
设⊙O的半径为R,DE=x,则
 ,
,
∵AB2+BC2=4R2,
∴(AB+BC)2=4R2+2•AB•BC=4R2+2(36-2R2)=72,
AB+BC=6 ,
,
又 ,
,
∴ (AB+BC)x=18,
(AB+BC)x=18,
则x=3 .
.
故答案为:3 .
.
点评:此题的难度较大,综合运用了圆周角定理的推论、勾股定理和图形的面积计算方法.
 ,再根据DE把四边形ABCD分割成的两部分的面积进行计算,即可求解.
,再根据DE把四边形ABCD分割成的两部分的面积进行计算,即可求解.解答:
 解:如图,连接BD,
解:如图,连接BD,因为AC是直径,
所以∠ADC=90°.
因为AD=DC,
所以∠ACD=45°,
所以∠ABD=45°,又∠DEB=90°,
所以△DEB为等腰直角三角形,
所以DE=BE.
设⊙O的半径为R,DE=x,则
 ,
,∵AB2+BC2=4R2,
∴(AB+BC)2=4R2+2•AB•BC=4R2+2(36-2R2)=72,
AB+BC=6
 ,
,又
 ,
,∴
 (AB+BC)x=18,
(AB+BC)x=18,则x=3
 .
.故答案为:3
 .
.点评:此题的难度较大,综合运用了圆周角定理的推论、勾股定理和图形的面积计算方法.

练习册系列答案
相关题目
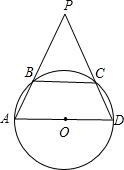 如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )| A、25π | B、16π | C、15π | D、13π |
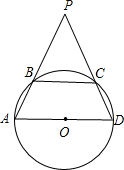 如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为
如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为