题目内容
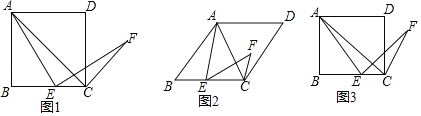
【题目】在△ABC中,![]() ,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作
,AC=4,BC=3,点D是斜边AB的中点. 以点D为顶点作![]() ,射线DM、DN分别交边AC、CB于点E、F.
,射线DM、DN分别交边AC、CB于点E、F.
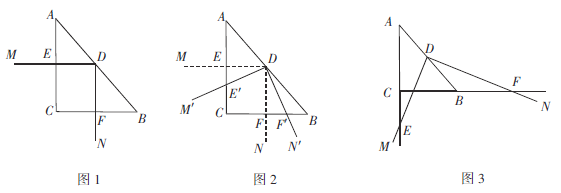
特例
(1)如图1,若![]() ,不添加辅助线,图1中所有与△ABC相似的三角形为 ,
,不添加辅助线,图1中所有与△ABC相似的三角形为 ,![]() ;
;
操作探究:
(2)将(1)中的![]() 从图1 的位置开始绕点D按逆时针方向旋转,得到
从图1 的位置开始绕点D按逆时针方向旋转,得到![]() .如图2,当射线
.如图2,当射线![]() 分别交边
分别交边![]() 于点
于点![]() 时,求
时,求![]() 的值;
的值;
拓展延伸:
(3)如图3,![]() 中,
中,![]() ,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作
,AC=m,BC=n,点D是斜边AB的中点,以点D为顶点作![]() ,射线
,射线![]() 分别交边
分别交边![]() 的延长线于点
的延长线于点![]() ,则
,则![]() 的值为_______________.(用含
的值为_______________.(用含![]() 的代数式表示,直接回答即可)
的代数式表示,直接回答即可)
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)证得四边形DECF为矩形,则DF∥AC,则![]() ,
,![]() ,又根据三角形中位线的性质,即可求得
,又根据三角形中位线的性质,即可求得![]() 的值;
的值;
(2)由旋转可知∠![]() ∠
∠![]() ,可证得
,可证得![]() ,由(1)的结论可求得答案;
,由(1)的结论可求得答案;
(3)作DG⊥AC于G,DH⊥BC于H,利用三角形中位线定理求得![]() ,
,![]() ,再证得
,再证得![]() ,即可求解.
,即可求解.
(1)∵DE∥BC,∠ACB=∠EDF=![]() ,
,
∴四边形DECF为矩形,
∴DF∥AC,
∴![]() ,
,![]() ;
;
∵点D是斜边AB的中点,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由旋转可知:∠![]() ∠
∠![]() ,且∠
,且∠![]() ∠
∠![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)得![]() ,
,
∴![]() ;
;
(3)作DG⊥AC于G,DH⊥BC于H,
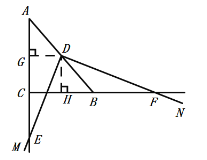
∵点D是斜边AB的中点,
∴![]() ,
,![]() ,
,
∵DG⊥AC,DH⊥BC,∠ACB=![]() ,
,
∴四边形DECF为矩形,
∴∠GDH=![]() ,
,
又∵∠MDN=![]() ,
,
∴∠GDE+∠EDH=∠HDF+∠EDH=![]() ,
,
∴∠GDE=∠HDF,
又∵∠DGE=∠DHF=![]() ,
,
∴![]() ,
,
∴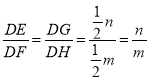 .
.

练习册系列答案
相关题目