��Ŀ����
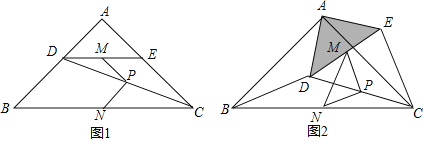
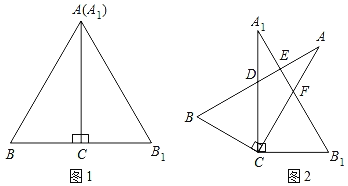
����Ŀ��������ȫ�ȵĺ�30���ǵ�ֱ�����ǰ尴��ͼ1��ʾ�ķ�ʽ���ã���֪��BAC����B1A1C��30�����̶����ǰ�A1B1C��Ȼ�����ǰ�ABC��ֱ�Ƕ���C˳ʱ����ת����ת��С��90��������ͼ2��ʾ��λ�ã�AB��A1C��A1B1�ֱ��ڵ�D��E��AC��A1B1���ڵ�F��
��1������ת�ǵ���20��ʱ����BCB1���� ������
��2������ת�ǵ��ڶ��ٶ�ʱ��AB��A1B1��ֱ����˵�����ɣ�
���𰸡���1��160����2������ת�ǵ���30��ʱ��AB��A1B1��ֱ�����ɼ�������
��������
��1����ת�ǡ�A1CA��20�㣬���ԡ�BCB1��90�㣫90��20�㣽160�㣻
��2����AB��A1B1��ֱʱ����A1ED��90�㣬������A1DE����������������������ʿ�֪��DCA����������ת�Ƕ�����
�⣺��1������ת�ǵ���20��ʱ�����A1CA��20����
���BCB1��90��+90����20����160����
�ʴ�Ϊ160��
��2������ת�ǵ���30��ʱ��AB��A1B1��ֱ���������£�
��AB��A1B1��ֱʱ����A1ED��90��
���A1DE��90������A1��90����30����60����
�ߡ�A1DE����A+��DCA��
���DCA��60����30����30����
������ת�ǵ���30��ʱ��AB��A1B1��ֱ��
�ʴ�Ϊ160��

 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�